Mostrando las entradas con la etiqueta resolucion de problemas. Mostrar todas las entradas
Mostrando las entradas con la etiqueta resolucion de problemas. Mostrar todas las entradas
17 de diciembre de 2019
Acertijos: las bolas blancas, las bolas negras y la muerte
El acertijo
Eres un preso que ha sido condenado a muerte. Pero te ofrecen una oportunidad de vivir si consigues jugar bien a este simple juego.
Te dan 50 bolas de mármol negras, 50 bolas blancas y dos cuencos vacíos.
Luego, te dicen: "Divide estas 100 bolas en estos dos cuencos. Puedes dividirlas de la forma que quieras mientras uses todas las bolas.
"Luego, te cubriremos los ojos y removeremos las bolas. Tendrás que elegir un cuenco y sacar una bola. Si es blanca, vivirás, pero si es negra...morirás".
¿Cómo tienes que dividir las bolas para que tengas las mayores probabilidades de elegir una bola blanca?
La solución
Pon una bola blanca en un cuenco y todas las demás en otro cuenco (49 blancas y 50 negras).
De esta forma empiezas con una probabilidad 50/50 de elegir el cuenco con solo la bola blanca, lo cual ¡te salvaría la vida instantáneamente!.
Pero incluso si eliges el otro cuenco, tendrás todavía una probabilidad de casi 50/50 de agarrar una de las 49 bolas blancas.
Fuente: BBC Mundo
12 de noviembre de 2019
Matemáticas: el problema de las pinturas de Mondrian
Los cuadros geométricos de Piet Mondrian, una de los máximops representantes del arte abstracto mundial, esconden mucha matemática... y tmbién este rimpecabezas, o problema, que les traemos a continuación.
El problema matemático de Mondrian consiste en dividir una cuadrícula de dimensiones n x n, en rectángulos y cuadrados de lados enteros e incongruentes entre sí (es decir, que no haya dos iguales), de tal modo que la diferencia entre la superficie del rectángulo mayor y el menor sea la menor posible. Esa resta dará la puntuación.
¿Cómo dijo?
Este enunciado, formulado de esta manera, en abstracto, resulta difícil de entender, pero se ve muy fácilmente con un caso concreto.
Por ejemplo, tomemos la cuadrícula de 4×4. Una posible solución es dividir el cuadro en dos rectángulos de 3×4 y 1×4, lo que otorga una puntuación de 8. Una forma de mejorar el resultado es dividir la cuadrícula en 3 rectángulos, lo que permite rebajar la puntuación a 6.
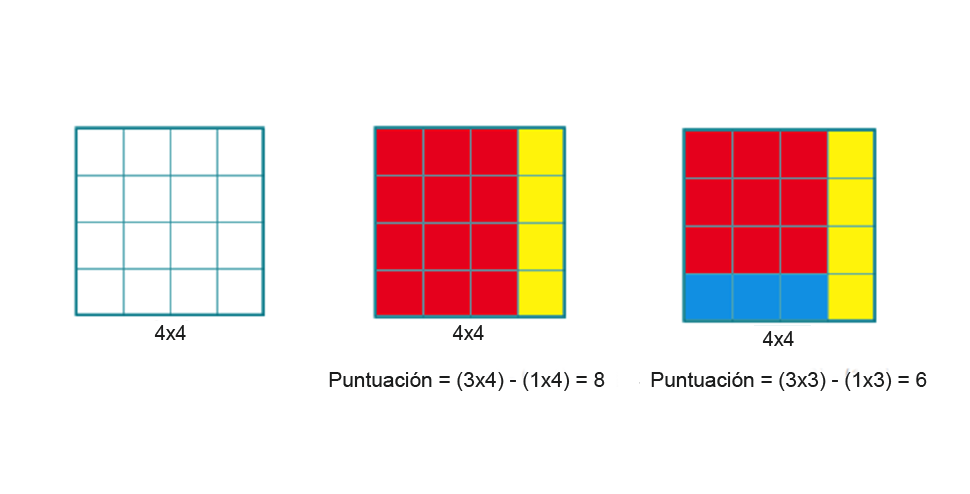
Pasatiempo N° 01:
Todavía hay una solución mejor para una cuadro 4×4, una distribución óptima que arroja una puntuación de 4. ¿Cuál es? Busca la respuesta.Fue a partir de 1915, luego de haber estudiado a profundiad los principios de movimientos como el impresionismo, el expresionismo o el cubismo, cuando Piet Mondrian comenzó a pintar sus famosos cuadros. Estas obras sublimaban la abstracción y simplificación de las formas hasta limitar los elementos a líneas rectas y rectángulos; y los colores empleados a los primarios (rojo, amarillo y azul) y los acromáticos (gris, blanco y negro). Con este lenguaje, el pintor trataba de reflejar el equilibrio de opuestos —líneas vs superficies; formas horizontales vs verticales; colores vivos vs ausencia de color— que gobernaban la naturaleza y el universo entero y que constituía su esencia y espíritu... ¡bastante profundo y ambicioso! ¿verdad?
Ahora vamos a dar un paso más, pasemos a la siguiente cuadrícula:
Pasatiempo 2:
Aquí se muestra la mejor solución para el caso de un cuadro de 5×5, que permite una Puntuación de 4.En el caso de un cuadro de 6×6, la mínima puntuación posible es 5, ¿cuál es la solución que permite alcanzar este valor?
¿Y cuál es la solución óptima para un cuadro de 8×8?

11 de noviembre de 2019
Matemática: Qué es la teoría de categorías y cómo se ha "puesto de moda"
Desde hace algunos años se habla mucho de una de las ramas de la matemática: la teoría de categorías que ha ganado bastante popularidad dentro de la comunidad matemática. Pero, ¿qué es esta rama de las matemáticas y por qué está de moda?
Algunas personas llaman a la teoría de categorías
“las matemáticas de las matemáticas”, ya que se sitúa por encima de
muchas disciplinas matemáticas, conectándolas. Fue propuesta en 1945
como una herramienta para trasladar problemas matemáticos de un campo a
otro, en el que se pudieran resolver con mayor facilidad. Por ejemplo,
sabemos que en cualquier momento debe haber un punto en la superficie de
la Tierra donde la velocidad del viento es cero. Pero para demostrar
este precioso resultado lo debemos traducir a una afirmación algebraica,
para lo que es útil emplear una pizca de teoría de categorías.
Habitualmente, resultados más complejos requieren más teoría de
categorías. La demostración del último teorema de Fermat, por ejemplo,
se basa en una gran cantidad de matemáticas del s. XX y la teoría de
categorías jugó allí también su papel.
Desafortunadamente, este alto nivel de abstracción
superó incluso el grado de tolerancia de los propios matemáticos y,
durante años, muchos de ellos han considerado esta teoría como un
“sinsentido abstracto” y se han limitado a usarla cuando era totalmente
necesario para su trabajo. Sin embargo, otros sí aceptaron con los
brazos abiertos la belleza y el poder de esta disciplina, lo que hizo
que su influencia fuese extendiéndose de forma gradual no solo en las
matemáticas, sino también en otras ciencias. A partir de la década de
1990 comenzó a infiltrarse en las ciencias de la computación: nuevos
lenguajes de programación como Haskell y Scla, por ejemplo, empleaban
ideas de la teoría de categorías. Actualmente aparecen nuevas
aplicaciones de esta teoría a la química, la ingeniería eléctrica o
¡incluso para diseñar frenos de los coches! La teoría de categorías aplicada, que en otra época hubiese sido considerada un oxímoron, se está convirtiendo en un tema de investigación real.
2 de junio de 2019
Argentina: investigadora ideó un libro para enseñar matemáticas con fútbol
Una materia que le ha costado a más de uno en la escuela y que podríamos entenderlo con algo tan sencillo como las reglas del fútbol, es posible gracia a un profesora santafesina.
Matemática es una asignatura obligatoria y fundamental en cualquier escuela y que se encuentra presente en nuestra vida diaria, aunque algunos no quieran admitirlo.
Muchos de nosotros hemos fallado en los cálculos, reprobamos la materia en la escuela, haciéndonos odiarla totalmente o simplemente no nos gustaba, porque parecia aburrida.
Por todo esto, una profesora tomó cartas en el asunto, para que las matemáticas puedan ser más llevaderas, entendibles y aplicables a temas generales.
Marilina Carena es licenciada en Matemáticas Aplicadas, profesora adjunta de la Facultad de Ingeniería Química de la UNL e investigadora adjunta del CONICET , que ideó un libro para enseñar matemáticas usando el futbol.
La santafesina logró relacionar temas que tiene que ver con el fútbol a operaciones matemáticas. En diálogo con Aire de Santa Fe, comentó cómo nació esta idea y en qué consiste.
“A mí sí me gustan las dos cosas, mucho. De tanto está con ambas cosas a la vez , note que tiene muchísimas cosas en común y entonces se me ocurrió en escribir algunos problemas y sus soluciones”.
Se determinó a mostrar como con la matemática se relacionaba un montón de conceptos de la escuela con temas referidos al fútbol.
“La idea es que ellos puedan, algunos conceptos que puedan trabajar en la escuela o bien, motivarlos o fijarlos a través de problemas que vengan involucrados por el lado del futbol que eso si manejan”, explicó la autora.
El libro titulado “La pelota siempre al 10” busca traducir las cosas que vieron en la matemática al lenguaje del fútbol o al revés y ver que son la misma cosa, el mismo razonamiento.
Los temas abarcan varios niveles de la escuela secundaria para que pueden desarrollarlos y los principales destinatarios son los docentes para que una herramienta de aprendizaje.
“Es un tema que despierta pasiones para por ese lado, ver si podemos motivar un poco a los chicos a que les guste más la matemáticas”.
El libro matemático contiene más de 70 problemas resueltos y casi 30 ejercicios y será presentado oficialmente el próximo mes de agosto.
Tomado de: El aire de Santa Fe
El Litoral
Matemática es una asignatura obligatoria y fundamental en cualquier escuela y que se encuentra presente en nuestra vida diaria, aunque algunos no quieran admitirlo.
Muchos de nosotros hemos fallado en los cálculos, reprobamos la materia en la escuela, haciéndonos odiarla totalmente o simplemente no nos gustaba, porque parecia aburrida.
Por todo esto, una profesora tomó cartas en el asunto, para que las matemáticas puedan ser más llevaderas, entendibles y aplicables a temas generales.
Marilina Carena es licenciada en Matemáticas Aplicadas, profesora adjunta de la Facultad de Ingeniería Química de la UNL e investigadora adjunta del CONICET , que ideó un libro para enseñar matemáticas usando el futbol.
La santafesina logró relacionar temas que tiene que ver con el fútbol a operaciones matemáticas. En diálogo con Aire de Santa Fe, comentó cómo nació esta idea y en qué consiste.
“A mí sí me gustan las dos cosas, mucho. De tanto está con ambas cosas a la vez , note que tiene muchísimas cosas en común y entonces se me ocurrió en escribir algunos problemas y sus soluciones”.
Se determinó a mostrar como con la matemática se relacionaba un montón de conceptos de la escuela con temas referidos al fútbol.
“La idea es que ellos puedan, algunos conceptos que puedan trabajar en la escuela o bien, motivarlos o fijarlos a través de problemas que vengan involucrados por el lado del futbol que eso si manejan”, explicó la autora.
El libro titulado “La pelota siempre al 10” busca traducir las cosas que vieron en la matemática al lenguaje del fútbol o al revés y ver que son la misma cosa, el mismo razonamiento.
Los temas abarcan varios niveles de la escuela secundaria para que pueden desarrollarlos y los principales destinatarios son los docentes para que una herramienta de aprendizaje.
“Es un tema que despierta pasiones para por ese lado, ver si podemos motivar un poco a los chicos a que les guste más la matemáticas”.
El libro matemático contiene más de 70 problemas resueltos y casi 30 ejercicios y será presentado oficialmente el próximo mes de agosto.
Tomado de: El aire de Santa Fe
El Litoral
9 de abril de 2019
Laura Sprechmann: “El método científico está siendo cuestionado”
La directiva de la entidad encargada de difundir el conocimiento de los Nobel alerta de la desconfianza y confusión general ante las investigaciones científicas.
Al entrar al edificio de Nobel Media, en Estocolmo, hay un pasillo repleto de estatuas en los laterales. Al final del mismo, está la de Alfred Nobel. El último testamento del inventor de la dinamita indicaba que su fortuna debía usarse para la creación de los premios que hoy llevan su nombre y reconocen la labor de profesionales en diferentes campos como la física, la química, o la medicina. En el mismo edificio, unas plantas más arriba, Laura Sprechmann, CEO de Nobel Media, recibe a EL PAÍS en una sala llena de retratos de los últimos ganadores de un premio Nobel. Entre ellos están el estadounidense James Allison y el japonés Tasuku Honjo, ambos ganadores del Nobel de Medicina en 2018, o Frances H. Arnold, premiada por su investigación en Química. "En los últimos años se ha producido una especie de erosión de lo que es un experto y una desconfianza o confusión general en la ciencia", afirma Sprechmann mientras observa las láminas pintadas cada año por el artista Niklas Elmehed.
Pero este reto no es nuevo: “Hemos tenido propaganda que suscitaba desconfianza hacia los científicos antes. Pero ahora tenemos los canales para comunicar y difundir todo de una manera totalmente distinta a como era hace 20, 50 o 100 años”. Para ella, la discusión sobre el clima es un buen ejemplo. “La ciencia está muy clara, pero mucha gente está divulgando información que no es cierta. Los métodos científicos hoy en día son cuestionados y se trata de una situación difícil teniendo en cuenta que el método científico está basado en el hecho de que siempre se deben cuestionar las cosas”, afirma.
Para enfrentarse a este desafío, considera primordial tener la capacidad de comunicar y presentar hechos. Recuerda cómo la voluntad de Alfred Nobel en su testamento de 1895 era otorgar premios a aquellos que llevasen a cabo "el mayor beneficio a la humanidad”. “Tenemos la obligación de contribuir con el conocimiento y fortalecer a las personas que quieren escuchar y aprender”, sostiene.
Con este objetivo, la entidad organiza desde 2012 en países de todo el mundo el Nobel Prize Dialogue. Se trata de un evento gratuito en el que varios premios Nobel y expertos debaten durante un día sobre los retos globales de la humanidad. Por ejemplo, sobre la energía, la inteligencia artificial, la comida, el agua, la educación o la verdad.
El 22 de mayo de este año tendrá lugar por primera vez en Madrid y se debatirá sobre el futuro del envejecimiento. Entre otros expertos, acudirán Edvard Moser, ganador del Nobel de Medicina en 2014, y Mario Vargas Llosa, Premio Nobel de Literatura en 2010. El escritor tendrá una conversación con el poeta Luis Alberto de Cuenca. “Se hablará sobre las pensiones, aspectos sociales como el cuidado de los mayores, la biología del envejecimiento, enfermedades como el cáncer o la demencia o cómo los robots pueden asistir a los mayores”. En el evento, organizado por Nobel Media junto a la Fundación Ramón Areces, no solo se abordarán aspectos negativos, también se debatirá sobre la creatividad y el aprendizaje en el envejecimiento.
Y se intentará dar respuestas a diversas preguntas: “¿Cuánto tiempo queremos vivir y si vamos a vivir más qué vamos a hacer con ese tiempo?”. España será el país del mundo con mayor esperanza de vida en 2040, según un estudio de la Universidad de Washington. El informe indica que los españoles llegarán a los 85,8, casi tres años por encima del promedio actual. “La edad de jubilación también es un debate, ya que tenemos vidas más saludables y hay ciertos trabajos donde no es necesario detenerse a cierta edad porque no requieren un esfuerzo físico”, afirma Sprechmann en una entrevista en Estocolmo en un viaje al que EL PAÍS ha sido invitado por el Instituto Sueco y la Embajada de Suecia en Madrid.
Además de compartir conocimiento, se pretende que los expertos puedan servir de referentes para los jóvenes. “Tienen historias personales tremendas. Si oyes que un premio Nobel de Química cuando iba a la escuela, sacaba malas notas en química y tú tienes 13 años, estás en el colegio y tienes problemas con la asignatura, pensarás que nada es imposible. Es la importancia de fallar y equivocarse”, cuenta la CEO de la Nobel Media.
El artículo completo en: El País (España)
Al entrar al edificio de Nobel Media, en Estocolmo, hay un pasillo repleto de estatuas en los laterales. Al final del mismo, está la de Alfred Nobel. El último testamento del inventor de la dinamita indicaba que su fortuna debía usarse para la creación de los premios que hoy llevan su nombre y reconocen la labor de profesionales en diferentes campos como la física, la química, o la medicina. En el mismo edificio, unas plantas más arriba, Laura Sprechmann, CEO de Nobel Media, recibe a EL PAÍS en una sala llena de retratos de los últimos ganadores de un premio Nobel. Entre ellos están el estadounidense James Allison y el japonés Tasuku Honjo, ambos ganadores del Nobel de Medicina en 2018, o Frances H. Arnold, premiada por su investigación en Química. "En los últimos años se ha producido una especie de erosión de lo que es un experto y una desconfianza o confusión general en la ciencia", afirma Sprechmann mientras observa las láminas pintadas cada año por el artista Niklas Elmehed.
Pero este reto no es nuevo: “Hemos tenido propaganda que suscitaba desconfianza hacia los científicos antes. Pero ahora tenemos los canales para comunicar y difundir todo de una manera totalmente distinta a como era hace 20, 50 o 100 años”. Para ella, la discusión sobre el clima es un buen ejemplo. “La ciencia está muy clara, pero mucha gente está divulgando información que no es cierta. Los métodos científicos hoy en día son cuestionados y se trata de una situación difícil teniendo en cuenta que el método científico está basado en el hecho de que siempre se deben cuestionar las cosas”, afirma.
Para enfrentarse a este desafío, considera primordial tener la capacidad de comunicar y presentar hechos. Recuerda cómo la voluntad de Alfred Nobel en su testamento de 1895 era otorgar premios a aquellos que llevasen a cabo "el mayor beneficio a la humanidad”. “Tenemos la obligación de contribuir con el conocimiento y fortalecer a las personas que quieren escuchar y aprender”, sostiene.
Con este objetivo, la entidad organiza desde 2012 en países de todo el mundo el Nobel Prize Dialogue. Se trata de un evento gratuito en el que varios premios Nobel y expertos debaten durante un día sobre los retos globales de la humanidad. Por ejemplo, sobre la energía, la inteligencia artificial, la comida, el agua, la educación o la verdad.
El 22 de mayo de este año tendrá lugar por primera vez en Madrid y se debatirá sobre el futuro del envejecimiento. Entre otros expertos, acudirán Edvard Moser, ganador del Nobel de Medicina en 2014, y Mario Vargas Llosa, Premio Nobel de Literatura en 2010. El escritor tendrá una conversación con el poeta Luis Alberto de Cuenca. “Se hablará sobre las pensiones, aspectos sociales como el cuidado de los mayores, la biología del envejecimiento, enfermedades como el cáncer o la demencia o cómo los robots pueden asistir a los mayores”. En el evento, organizado por Nobel Media junto a la Fundación Ramón Areces, no solo se abordarán aspectos negativos, también se debatirá sobre la creatividad y el aprendizaje en el envejecimiento.
Y se intentará dar respuestas a diversas preguntas: “¿Cuánto tiempo queremos vivir y si vamos a vivir más qué vamos a hacer con ese tiempo?”. España será el país del mundo con mayor esperanza de vida en 2040, según un estudio de la Universidad de Washington. El informe indica que los españoles llegarán a los 85,8, casi tres años por encima del promedio actual. “La edad de jubilación también es un debate, ya que tenemos vidas más saludables y hay ciertos trabajos donde no es necesario detenerse a cierta edad porque no requieren un esfuerzo físico”, afirma Sprechmann en una entrevista en Estocolmo en un viaje al que EL PAÍS ha sido invitado por el Instituto Sueco y la Embajada de Suecia en Madrid.
Además de compartir conocimiento, se pretende que los expertos puedan servir de referentes para los jóvenes. “Tienen historias personales tremendas. Si oyes que un premio Nobel de Química cuando iba a la escuela, sacaba malas notas en química y tú tienes 13 años, estás en el colegio y tienes problemas con la asignatura, pensarás que nada es imposible. Es la importancia de fallar y equivocarse”, cuenta la CEO de la Nobel Media.
El artículo completo en: El País (España)
12 de octubre de 2018
Una astrofísica explica lo que tendrían que haber hecho los personajes de Friends para subir el sofá de Ross por las escaleras
En una de las escenas más icónicas de la quinta temporada de Friends, Rachel y Chandler ayudan a Ross a subir su nuevo sofá por las escaleras. La escena es icónica porque uno puede verse reflejado en ella: quién no ha ayudado a un amigo a regañadientes con una mudanza y se ha encontrado con que el sofá no cabe en el ascensor o no dobla una esquina difícil.
En Friends, el trío se encuentra con una de esas esquinas difíciles y nunca consigue pasar del rellano, así que Ross acaba devolviendo el mueble. Pero en realidad Ross se rinde demasiado rápido. La doctora en astrofísica Caroline Zunckel ha analizado la escena y asegura que el sofá cabía perfectamente por las escaleras: solo había que aplicar el teorema de Pitágoras e inclinar el sofá en un ángulo determinado para doblar la esquina. El blog de SpaceRoom lo explica paso a paso en una infografía:
- Medir la anchura de las escaleras (WS), así como el ancho (WC) y el largo (LC) del sofá.
- Usar la ecuación T = 44,15064 - (11,94274 × WS) + (8,69119 × WC) + (3,65961 × LC) para calcular el ángulo en el que habrá que rotar el sofá durante el paso 4.
- Subir el sofá por las escaleras tan alto como sea posible.
- Usar el ángulo calculado en el paso 2 para inclinar el sofá hacia el techo. De esta forma, el sofá puede girar la esquina sin bloquearse.
- Una vez superada la esquina, volver a la inclinación original para que el sofá esté de nuevo en paralelo a las escaleras y subir hasta el apartamento.
- Sentarse en el sofá a disfrutarlo con una cerveza fría. (Opcional: ofrecer una a tus amigos por ayudarte con él).
4 de junio de 2018
Combinatorio, dados y probabilidades
¿Cómo se puede hacer un calendario perpetuo con dos dados de seis caras?
Los datos del acertijo final de la semana pasada parecen muy insuficientes para sacar cualquier conclusión; sin embargo, hay pocos desarrollos del torneo de ajedrez imaginario que den lugar a un descenso del 5% en el porcentaje de victorias de Kaspárov. Reproduzco la acertada respuesta de nuestro “usuario destacado” Manuel Amorós:
Los datos del acertijo final de la semana pasada parecen muy insuficientes para sacar cualquier conclusión; sin embargo, hay pocos desarrollos del torneo de ajedrez imaginario que den lugar a un descenso del 5% en el porcentaje de victorias de Kaspárov. Reproduzco la acertada respuesta de nuestro “usuario destacado” Manuel Amorós:
Teniendo en cuenta que el 5% es 1/20,
tendríamos que hallar dos fracciones propias que restadas dieran como
resultado 1/20. Seguramente, el primer par de fracciones que cumplen son
1/4 y 1/5, ya que 1/4 – 1/5 = 1/20. Pero estas proporciones no se
ajustan al hecho de que Kaspárov tenía ventaja inicial sobre su rival.
El siguiente par de fracciones serían 4/5 y 6/8: 4/5 – 6/8 = 1/20
Es decir, que una posible respuesta es
que Kaspárov empezó ganando 4 de 5 partidas (descontadas las tablas) y
después ganó dos partidas y perdió una, reduciéndose de ese modo su
porcentaje de triunfos en un 5% exacto.
El problema de las tres tarjetas
(una con dos caras rojas, una con dos caras blancas y una con una cara
roja y otra blanca) sigue propiciando un animado debate (ver comentarios
de la semana pasada). Como señalé en el artículo anterior, es fácil
pensar que si nos muestran una cara roja, la probabilidad de que la otra
cara también sea roja es 1/2; pero en realidad hay tres posibilidades
equiprobables: que nos muestren una cara de la tarjeta RR, que nos
muestren la otra cara de RR o que nos muestren la cara roja de la
tarjeta RB; en dos de estos tres casos la otra cara es roja, por tanto
la probabilidad pedida es 2/3.
La combinatoria de los dados
La probabilidad de un suceso expresa
la relación entre los casos favorables y los casos posibles. Decimos que
la probabilidad de sacar un 5 al lanzar un dado es 1/6 porque el dado
tiene seis caras (casos posibles) y solo en una de esas caras hay un 5
(casos favorables). Este es un ejemplo trivial, pero a menudo el cálculo
de probabilidades implica la resolución previa de problemas
combinatorios no siempre sencillos para determinar el número de casos
posibles y de casos favorables.
La probabilística de un solo dado es
trivial, pero con dos dados la cosa empieza a complicarse y es fácil
incurrir en errores de apreciación. Al lanzar dos dados y sumar sus
puntos podemos obtener las puntuaciones comprendidas entre 2 y 12: once
posibilidades, por lo que podría parecer que la probabilidad de sacar
una puntuación concreta, por ejemplo 7, es 1/11; pero este razonamiento
es erróneo, pues las once posibilidades no son equiprobables; hay una
sola forma de obtener 12 puntos (6-6) y seis formas de obtener 7 (6-1,
5-2, 4-3, 3-4, 2-5, 1-6). Cada una de las seis caras de un dado puede
emparejarse con cada una de las seis caras del otro, por lo que hay 6 x 6
= 36 parejas posibles, de la que solo una da 12 puntos y seis dan 7
puntos; por tanto, la probabilidad de obtener 12 puntos es 1/36 y la de
sacar 7 puntos es 6/36 = 1/6.
Si en vez de puntos en las caras de
los dos dados figuraran los dígitos del 1 al 6, adosándolos podríamos
formar los números 11 a 16, 21 a 26, 31 a 36…, 61 a 66. ¿Podemos numerar
las caras de dos dados de manera que adosándolos convenientemente se
puedan formar todos los días del mes? Hay que usar siempre los dos
dados, expresando los números de una sola cifra de la forma 01, 02, etc.
Naturalmente, la cosa se complica a
medida que aumenta el número de dados. ¿Cuál es la probabilidad de sacar
un póquer a la primera con los dados de póquer (valga la redundancia)?
¿Y la de sacar un repóquer?
Fuente:
1 de junio de 2018
Martin Gardner y la diversión matemática
Los retos matemáticos han cautivado a las mentes brillantes de la
historia. Y más recientemente, atraparon al público, en gran parte
gracias a la labor de Martin Gardner, que popularizó problemas de matemática y lógica como estos:
1. ¿Puedes trazar cuatro líneas rectas, sin levantar la punta del lápiz del papel, que pasen por los nueve puntos de la ilustración?

2. ¿Con cuánta rapidez puedes multiplicar estos números?
256 x 3 x 45 x 3961 x 77 x 488 x 2809 x 0
3. ¿Puedes elegir seis dígitos de la ilustración que sumados den 21?

Dejaremos para el final las soluciones. Estos acertijos se pueden resolver nada más verlos en la pantalla, si uno es capaz de pensar diferente, o desistir después de darle muchas vueltas a la cabeza… ¿Para qué sirven los problemas matemáticos? Para Martin Gardner (1914-2010) era una forma de despertar el interés de la gente por las matemáticas. Así lo contaba en la revista Scientific American, donde se pasó más de veinte años publicando una columna mensual sobre juegos matemáticos: «Con seguridad, el mejor camino para despertar a un estudiante consiste en ofrecerle un intrigante juego, puzzle, truco de magia, chiste, paradoja, pareado de naturaleza matemática… o cualquiera de entre una veintena de cosas que los profesores aburridos tienden a evitar porque parecen frívolas».
El artículo completo en: Open Mind

1. ¿Puedes trazar cuatro líneas rectas, sin levantar la punta del lápiz del papel, que pasen por los nueve puntos de la ilustración?

2. ¿Con cuánta rapidez puedes multiplicar estos números?
256 x 3 x 45 x 3961 x 77 x 488 x 2809 x 0
3. ¿Puedes elegir seis dígitos de la ilustración que sumados den 21?

Dejaremos para el final las soluciones. Estos acertijos se pueden resolver nada más verlos en la pantalla, si uno es capaz de pensar diferente, o desistir después de darle muchas vueltas a la cabeza… ¿Para qué sirven los problemas matemáticos? Para Martin Gardner (1914-2010) era una forma de despertar el interés de la gente por las matemáticas. Así lo contaba en la revista Scientific American, donde se pasó más de veinte años publicando una columna mensual sobre juegos matemáticos: «Con seguridad, el mejor camino para despertar a un estudiante consiste en ofrecerle un intrigante juego, puzzle, truco de magia, chiste, paradoja, pareado de naturaleza matemática… o cualquiera de entre una veintena de cosas que los profesores aburridos tienden a evitar porque parecen frívolas».
El artículo completo en: Open Mind

26 de marzo de 2018
Si quieres resolver un problema con alguien, sigue estos cuatro pasos
La violencia es la expresión trágica de necesidades no satisfechas.
En ocasiones los conflictos se enquistan porque no hemos sabido ver lo que la otra persona necesita. Cuando esto ocurre, el otro se enfada o llega a tener comportamientos agresivos aunque no sepa el por qué. Sencillamente, deja de hablarnos, nos grita o actúa con cualquier otra respuesta que tenga en su catálogo habitual. En esos momentos, si decimos “no te enfades” conseguimos lo contrario, que el otro aún se cabree más. Por tanto, reconducir un conflicto requiere un modo diferente de comunicación. Así lo comprobó Marshall B. Rosenberg después de trabajar en situaciones realmente complicadas durante los años 60 en el sur de Estados Unidos. Allí reinaba la segregación racial y los actos de violencia estaban a la orden del día. Este psicólogo desarrolló una metodología denominada Comunicación No Violenta (CNV), que le permitió acercar posiciones y reducir la agresividad de ambos bandos. Y dicha metodología podemos aplicarla en nuestro día a día cuando nos enfrentamos a una discusión o a un conflicto.
La CNV parte del supuesto de que el enfado, la agresividad o la violencia, en último extremo, son expresiones de la desesperación o de la impotencia de alguien ante una necesidad no atendida. Por ello, una comunicación efectiva ha de ver más allá de las palabras, de los hechos o de las emociones (aunque algunas nos saquen de quicio). Ha de reparar en las necesidades de fondo que existen y que no están satisfechas, para conseguir una conexión sincera con el otro y con uno mismo. Y eso es lo que propone la CNV, a través de cuatro fases.
La primera fase consiste en observar la situación sin juicio, tanto lo que ocurre fuera como lo que se nos mueve dentro. Una conversación reparadora comenzaría con una exposición sin valoración. No consiste en frases que le hagan al otro sacar el escudo defensivo como, por ejemplo: “trabajas demasiado”, “eres un desastre” o “te enfadas con cualquier tontería”. La idea es comenzar con algo que no se puede cuestionar, como: “cuando te hablo de algo importante para mí y coges el móvil para consultar tu correo…”. Si ha pasado, no se puede negar.
Lea el artículo completo en:
El País (España)
En ocasiones los conflictos se enquistan porque no hemos sabido ver lo que la otra persona necesita. Cuando esto ocurre, el otro se enfada o llega a tener comportamientos agresivos aunque no sepa el por qué. Sencillamente, deja de hablarnos, nos grita o actúa con cualquier otra respuesta que tenga en su catálogo habitual. En esos momentos, si decimos “no te enfades” conseguimos lo contrario, que el otro aún se cabree más. Por tanto, reconducir un conflicto requiere un modo diferente de comunicación. Así lo comprobó Marshall B. Rosenberg después de trabajar en situaciones realmente complicadas durante los años 60 en el sur de Estados Unidos. Allí reinaba la segregación racial y los actos de violencia estaban a la orden del día. Este psicólogo desarrolló una metodología denominada Comunicación No Violenta (CNV), que le permitió acercar posiciones y reducir la agresividad de ambos bandos. Y dicha metodología podemos aplicarla en nuestro día a día cuando nos enfrentamos a una discusión o a un conflicto.
La CNV parte del supuesto de que el enfado, la agresividad o la violencia, en último extremo, son expresiones de la desesperación o de la impotencia de alguien ante una necesidad no atendida. Por ello, una comunicación efectiva ha de ver más allá de las palabras, de los hechos o de las emociones (aunque algunas nos saquen de quicio). Ha de reparar en las necesidades de fondo que existen y que no están satisfechas, para conseguir una conexión sincera con el otro y con uno mismo. Y eso es lo que propone la CNV, a través de cuatro fases.
La primera fase consiste en observar la situación sin juicio, tanto lo que ocurre fuera como lo que se nos mueve dentro. Una conversación reparadora comenzaría con una exposición sin valoración. No consiste en frases que le hagan al otro sacar el escudo defensivo como, por ejemplo: “trabajas demasiado”, “eres un desastre” o “te enfadas con cualquier tontería”. La idea es comenzar con algo que no se puede cuestionar, como: “cuando te hablo de algo importante para mí y coges el móvil para consultar tu correo…”. Si ha pasado, no se puede negar.
Lea el artículo completo en:
El País (España)
15 de enero de 2018
Cómo Alcuino de York, "el hombre más sabio del mundo", forjó la base para la computadora hace 1.200 años
Temprano una mañana, sales para el
mercado. Vas a vender un lobo, una cabra y una col. El camino es
escabroso y peligroso, y tú tienes que vigilar constantemente al lobo
para que no se coma a la cabra, y a la cabra, para que no se coma la
col.
¿Cómo haces para pasar todo al otro lado sin que nada termine en el estómago de tus dos animales?
En el primer viaje, tienes que llevarte la cabra en el bote. Regresas y te llevas el lobo, lo dejas en la otra orilla pero te traes la cabra, a la que dejas donde empezaste para traer la col y finalmente, puedes traer la cabra contigo.
Probablemente ya conocías esta prueba de ingenio... es vieja, pero ¿sabes cuán vieja? Está registrada en un documento del siglo IX, el período que los historiadores solían llamar "los años oscuros".
El responsable es Alcuino, un personaje poco conocido que desafía la mala reputación de ese opaco y distante período de la historia europea. Es el autor de un libro de acertijos matemáticos en latín, llamado "Problemas para afinar el ingenio de los jóvenes".
El principio del Medioevo fue mucho más vibrante intelectualmente de lo que uno imaginaría dado el estereotipo, y la historia de Alcuino con sus acertijos matemáticos ayuda a aclarar esa imagen.
Cuando Alcuino nació cerca de York alrededor del año 732 d.C., Inglaterra era una colección de reinos sajones. Pero había reinos cristianos, un legado de la invasión romana.
York tenía una gran catedral con una escuela en la que Alcuino estudió, luego enseñó y finalmente dirigió. Bajo su administración, el colegio se convirtió en uno de los más distinguidos de Europa.
Coleccionaba libros en una renombrada biblioteca, así como obras de los Padres de la Iglesia Cristiana, que contenían fragmentos de la sabiduría de los griegos y romanos.
Lea el artículo completo en:
BBC Mundo
24 de diciembre de 2017
Conrad Wolfram: “El 80% de lo que se aprende en la asignatura de matemáticas no sirve para nada”
Conrad Wolfram, físico que está cambiando la forma de enseñar matemáticas en Estonia, apuesta por eliminar el cálculo a mano.
Conrad Wolfram (Oxford, 1970) piensa que tenemos un problema con las matemáticas. Nadie está contento: los estudiantes creen que es una asignatura difícil y sin interés, los maestros están frustrados con los resultados de sus alumnos y los gobiernos se dan cuenta de que son determinantes para la economía pero no saben cómo actualizar los programas académicos. "Cada vez vivimos en un mundo más matemático y sin embargo la educación está estancada", opina Wolfram, físico y matemático por la Universidad de Cambridge y fundador de Computer Based Math, una compañía centrada en rediseñar la asignatura de matemáticas que hace dos años lanzó su programa piloto en colaboración con el Gobierno de Estonia.
En 2010 Wolfram atrajo la atención de educadores y expertos en educación de diferentes partes del mundo con su charla TED Cómo enseñar a los niños matemáticas del mundo real, con más de 1,5 millones de reproducciones, en la que analiza los motivos por los que los estudiantes han perdido el interés en la asignatura que está detrás de las "creaciones más emocionantes de la humanidad", desde los cohetes hasta los mercados de valores.
Demasiadas horas de clase invertidas en aprender a calcular grandes divisiones y ecuaciones a mano. Ese es el gran fallo, según Wolfram, que apuesta por introducir la computación en las clases y dejar que sean las máquinas las que se encarguen del cálculo.
Pregunta. Si los niños no aprenden a calcular a mano y hacen las operaciones con el ordenador, ¿cómo van a entender lo que están haciendo?
Respuesta. Los matemáticos me odiarán por decir esto, pero antes de los ordenadores las matemáticas no eran muy útiles para el día a día, para la vida en general. Para cualquier campo en el que se usen muchos datos, como la física, la biología o la salud, la computación ha elevado las matemáticas a un estadio nuevo. Los problemas reales del siglo XXI solo se pueden resolver usando los ordenadores y por eso deben entrar en el sistema educativo como parte fundamental de la asignatura de matemáticas. Tener a los niños en las aulas calculando a mano ecuaciones de segundo grado ya no tiene sentido; hay que enseñarles a interpretar los datos y a sacar utilidad de las matemáticas. Enseñarles el funcionamiento básico está bien, pero complicarlo hasta la extenuación es una estrategia errónea que les aleja para toda la vida. Suelo poner el ejemplo de la conducción; no hace falta entender el funcionamiento de los motores para manejar un vehículo.
P. Algunos expertos sostienen que el cálculo ayuda a aprender el sentido de los números y es una buena herramienta para entrenarse en la toma de decisiones.
R. ¿Cuándo fue la última vez que multiplicaste 3/17 por 2/15? Probablemente lo aprendieras en la escuela pero nunca lo has vuelto a ejecutar. Muchos expertos dirán que multiplicando fracciones estás aprendiendo, pero solo estás recordando un proceso. Realmente no estás entendiendo para qué lo haces ni para qué sirve. Un ejemplo muy simple: en la ecuación x+2=4 te enseñaron que si pasas el dos a la derecha cambia de signo y se convierte en menos 2. Ahí tampoco entiendes qué estás haciendo. Las matemáticas tradicionales ya no tienen sentido y probablemente el 80% del contenido de la asignatura no es útil y nunca lo usarás fuera del aula.
P. Podrían decirle que dejarle el cálculo al ordenador en edad de aprender es de vagos.
R. Intentar saber cómo usar la computación no supone menos trabajo para el cerebro. Todo lo contrario. Los problemas a resolver son mucho más complejos y ahí es donde hay que entrenar a los niños. La programación es lo que equivaldría hoy al cálculo a mano, saber decirle al ordenador con códigos y números lo que tiene que hacer de forma muy precisa. Matemáticas, programación y pensamiento computacional deben ser la misma asignatura.
P. ¿Podría poner un ejemplo de esas situaciones de la vida real de las que habla?
R. Si te muestro los datos de dos webs y te pregunto cuál está funcionando mejor la primera pregunta que debes hacerte es qué significa mejor. Puede ser el tiempo que los usuarios pasan en cada una de ellas o las veces que hacen clic en alguna de las pestañas... En el mundo real puedes usar el machine learning o el análisis estadístico para medir y analizar resultados. Elegir qué opción funciona mejor en cada caso es complicado y ese tipo de conocimientos no se enseñan en la escuela. Las matemáticas son mucho más que el cálculo, aunque es comprensible que durante cientos de años se le haya dado tanta importancia, pues solo había una forma de hacerlo; a mano. Las matemáticas se han liberado del cálculo, pero esa liberación todavía no ha llegado a la educación.
P. Su empresa ha reinventado la asignatura de matemáticas para introducir la computación y ha introducido nuevas habilidades a evaluar como la comunicación matemática. ¿Cómo consiguió convencer al Gobierno de Estonia para implantarla en los colegios públicos?
R. Con 1,3 millones de habitantes, Estonia se considera el país más digital de Europa. Sus ciudadanos pueden votar, pagar impuestos, comprobar archivos médicos o registrar una empresa desde su ordenador de casa en pocos minutos. En el último informe PISA superó a los finlandeses en ciencias y matemáticas y es el nuevo referente en Europa en innovación educativa. Hace tres años conocí en unas jornadas a su Ministro de Educación, que es físico, y dos años después lanzamos el primer proyecto piloto, que se está usando en el 10% de los colegios públicos del país. Hemos centrado la asignatura, para estudiantes de Secundaria, en probabilidad y estadística y hemos cambiado el sistema de evaluación. Los alumnos aprenden a resolver cuestiones reales como por ejemplo ¿son las chicas mejores en matemáticas? o ¿mi estatura está en la media?. Ahora estamos en conversaciones con Irlanda y Australia.
El artículo completo en:
El País (España)
Conrad Wolfram (Oxford, 1970) piensa que tenemos un problema con las matemáticas. Nadie está contento: los estudiantes creen que es una asignatura difícil y sin interés, los maestros están frustrados con los resultados de sus alumnos y los gobiernos se dan cuenta de que son determinantes para la economía pero no saben cómo actualizar los programas académicos. "Cada vez vivimos en un mundo más matemático y sin embargo la educación está estancada", opina Wolfram, físico y matemático por la Universidad de Cambridge y fundador de Computer Based Math, una compañía centrada en rediseñar la asignatura de matemáticas que hace dos años lanzó su programa piloto en colaboración con el Gobierno de Estonia.
En 2010 Wolfram atrajo la atención de educadores y expertos en educación de diferentes partes del mundo con su charla TED Cómo enseñar a los niños matemáticas del mundo real, con más de 1,5 millones de reproducciones, en la que analiza los motivos por los que los estudiantes han perdido el interés en la asignatura que está detrás de las "creaciones más emocionantes de la humanidad", desde los cohetes hasta los mercados de valores.
Demasiadas horas de clase invertidas en aprender a calcular grandes divisiones y ecuaciones a mano. Ese es el gran fallo, según Wolfram, que apuesta por introducir la computación en las clases y dejar que sean las máquinas las que se encarguen del cálculo.
Pregunta. Si los niños no aprenden a calcular a mano y hacen las operaciones con el ordenador, ¿cómo van a entender lo que están haciendo?
Respuesta. Los matemáticos me odiarán por decir esto, pero antes de los ordenadores las matemáticas no eran muy útiles para el día a día, para la vida en general. Para cualquier campo en el que se usen muchos datos, como la física, la biología o la salud, la computación ha elevado las matemáticas a un estadio nuevo. Los problemas reales del siglo XXI solo se pueden resolver usando los ordenadores y por eso deben entrar en el sistema educativo como parte fundamental de la asignatura de matemáticas. Tener a los niños en las aulas calculando a mano ecuaciones de segundo grado ya no tiene sentido; hay que enseñarles a interpretar los datos y a sacar utilidad de las matemáticas. Enseñarles el funcionamiento básico está bien, pero complicarlo hasta la extenuación es una estrategia errónea que les aleja para toda la vida. Suelo poner el ejemplo de la conducción; no hace falta entender el funcionamiento de los motores para manejar un vehículo.
P. Algunos expertos sostienen que el cálculo ayuda a aprender el sentido de los números y es una buena herramienta para entrenarse en la toma de decisiones.
R. ¿Cuándo fue la última vez que multiplicaste 3/17 por 2/15? Probablemente lo aprendieras en la escuela pero nunca lo has vuelto a ejecutar. Muchos expertos dirán que multiplicando fracciones estás aprendiendo, pero solo estás recordando un proceso. Realmente no estás entendiendo para qué lo haces ni para qué sirve. Un ejemplo muy simple: en la ecuación x+2=4 te enseñaron que si pasas el dos a la derecha cambia de signo y se convierte en menos 2. Ahí tampoco entiendes qué estás haciendo. Las matemáticas tradicionales ya no tienen sentido y probablemente el 80% del contenido de la asignatura no es útil y nunca lo usarás fuera del aula.
P. Podrían decirle que dejarle el cálculo al ordenador en edad de aprender es de vagos.
R. Intentar saber cómo usar la computación no supone menos trabajo para el cerebro. Todo lo contrario. Los problemas a resolver son mucho más complejos y ahí es donde hay que entrenar a los niños. La programación es lo que equivaldría hoy al cálculo a mano, saber decirle al ordenador con códigos y números lo que tiene que hacer de forma muy precisa. Matemáticas, programación y pensamiento computacional deben ser la misma asignatura.
P. ¿Podría poner un ejemplo de esas situaciones de la vida real de las que habla?
R. Si te muestro los datos de dos webs y te pregunto cuál está funcionando mejor la primera pregunta que debes hacerte es qué significa mejor. Puede ser el tiempo que los usuarios pasan en cada una de ellas o las veces que hacen clic en alguna de las pestañas... En el mundo real puedes usar el machine learning o el análisis estadístico para medir y analizar resultados. Elegir qué opción funciona mejor en cada caso es complicado y ese tipo de conocimientos no se enseñan en la escuela. Las matemáticas son mucho más que el cálculo, aunque es comprensible que durante cientos de años se le haya dado tanta importancia, pues solo había una forma de hacerlo; a mano. Las matemáticas se han liberado del cálculo, pero esa liberación todavía no ha llegado a la educación.
P. Su empresa ha reinventado la asignatura de matemáticas para introducir la computación y ha introducido nuevas habilidades a evaluar como la comunicación matemática. ¿Cómo consiguió convencer al Gobierno de Estonia para implantarla en los colegios públicos?
R. Con 1,3 millones de habitantes, Estonia se considera el país más digital de Europa. Sus ciudadanos pueden votar, pagar impuestos, comprobar archivos médicos o registrar una empresa desde su ordenador de casa en pocos minutos. En el último informe PISA superó a los finlandeses en ciencias y matemáticas y es el nuevo referente en Europa en innovación educativa. Hace tres años conocí en unas jornadas a su Ministro de Educación, que es físico, y dos años después lanzamos el primer proyecto piloto, que se está usando en el 10% de los colegios públicos del país. Hemos centrado la asignatura, para estudiantes de Secundaria, en probabilidad y estadística y hemos cambiado el sistema de evaluación. Los alumnos aprenden a resolver cuestiones reales como por ejemplo ¿son las chicas mejores en matemáticas? o ¿mi estatura está en la media?. Ahora estamos en conversaciones con Irlanda y Australia.
El artículo completo en:
El País (España)
1 de diciembre de 2017
¿Cuáles son los países donde los niños trabajan mejor en equipo, según la nueva prueba PISA?
¿Están cumpliendo los planes escolares con las necesidades de los niños?
Los sistemas de estudio y de exámenes normalmente recompensan los logros individuales de los estudiantes.
Pero cuando entran al mundo laboral, se les hace hincapié en la importancia de las habilidades sociales y en la necesidad de cooperar con otra gente para solucionar problemas.
El Programa para la Evaluación Internacional de los Alumnos (PISA, por sus siglas en inglés) evalúa las habilidades de los estudiantes en lectura, matemáticas y ciencia.
Y por primera vez ha realizado una prueba global que mide las habilidades para resolver problemas de manera colaborativa.
Como era esperable, los alumnos sobresalientes en las pruebas académicas también tienden a ser mejores en la solución de dificultades en colaboración con otros.
Además son más hábiles para interpretar información y realizar razonamientos complejos, lo que los prepara mejor para enfrentar cualquier tipo de problemas.
Eso es válido en los diferentes países. Las naciones con mejor desempeño en pruebas académicas como Japón, Corea del Sur, Singapur, Estonia, Finlandia y Canadá son asimismo los que tienen mejores resultados resolviendo dificultades en conjunto.
Pero no en todos los casos. Los estudiantes de China, que son muy buenos en matemáticas y ciencias, se ubican dentro del promedio en cuanto a habilidades de colaboración.
En los 20 primeros lugares no aparece ningún país de América Latina que sobresalga en trabajo en equipo.
Los 20 países que mejor resuelven problemas en conjunto son:
- Singapur
- Japón
- Hong Kong
- Corea del Sur
- Canadá
- Estonia
- Finlandia
- Macao
- Nueva Zelanda
- Australia
- Taiwán
- Alemania
- Estados Unidos
- Dinamarca
- Reino Unido
- Holanda
- Suecia
- Austria
- Noruega
- Eslovenia
BBC Ciencia
Tags:
cooperacion,
educacion,
equipo,
habilidades sociales,
PISA,
problemas,
pruebas PISA,
resolucion de problemas,
trabajo en equipo
27 de noviembre de 2017
Entrena tu mente con un acertijo: ¿cómo puedes medir 1 litro con estas jarras y no desperdiciar la leche?
Vamos a poner a prueba tus neuronas. Con este sencillo acertijo, sencillo pero muy desafiante...
Un repartidor de leche tiene dos jarras vacías: una con una capacidad de 3 litros y la otra de 5 litros.
¿Cómo puede este lechero medir exactamente 1 litro sin desperdiciar la leche?
Baja para descubrir la respuesta
Posteriormente, llenó nuevamente la jarra de 3 litros y la usó para llenar la jarra de los 5 litros completamente.
La leche que quedó en la jarra de los 3 litros era 1 litro exactamente.
Tomado de: BBC
Un repartidor de leche tiene dos jarras vacías: una con una capacidad de 3 litros y la otra de 5 litros.
¿Cómo puede este lechero medir exactamente 1 litro sin desperdiciar la leche?
Baja para descubrir la respuesta
La respuesta
El lechero llenó la jarra con capacidad de 3 litros y después vació el contenido en la jarra de 5 litros.Posteriormente, llenó nuevamente la jarra de 3 litros y la usó para llenar la jarra de los 5 litros completamente.
La leche que quedó en la jarra de los 3 litros era 1 litro exactamente.
Tomado de: BBC
20 de abril de 2015
El problema matemático del que todo el mundo está hablando (desde Singapur, con amor)
Así dice el problema:
Albert y Bernard se acaban de hacer amigos de Cheryl y quieren saber cuándo es su cumpleaños. Cheryl les da una lista con 10 posibles fechas
Mayo 15, Mayo 16, Mayo 19
Junio 17, Junio 18
Julio 14, Julio 16
Agosto 14, Agosto 15, Agosto 17
Luego Cheryl les dice por separado a Albert y a Bernard, el mes y el día respectivamente.
-Albert: "No sé cuándo es el cumpleaños de Cheryl, pero sé que Bernard tampoco lo sabe".
-Bernard: "Al principio no sabía cuándo era el cumpleaños de Cheryl, pero ahora ya lo sé".
-Albert: "Entonces yo también sé cuándo es su cumpleaños".
¿Cuándo es el cumpleaños de Cheryl?
Tomado de:
17 de agosto de 2014
10 acertijos clásicos que pondrán a prueba tu capacidad lógica
Por pensamiento lateral se conoce una forma de pensamiento que consiste en solucionar problemas de una forma creativa. El término fue acuñado por Edward de Bono en el año 1967, en el libro New Think: the Use of Lateral Thinking.
Se han diseñado diversos acertijos que, presentados como un problema
tradicional, ponen a prueba los principios lógicos del que ha de
resolverlos. Se trata de, como se dice en inglés, de “pensar fuera de la caja”.
A continuación presentamos algunos de los acertijos clásicos
relacionados con esta manera de pensar. No te preocupes: aunque la
respuesta parezca evidente una vez conocida, no resulta tan sencillo
adivinarla si no hemos sido capaces de encontrar la clave para
responderla.
¿Cuántas has contestado correctamente (sin hacer trampas y mirar la respuesta)?

RESPUESTAS
Respuesta 1. Una de dos euros y otra de un euro. El padre de Juan le dice a su hijo que una de ellas no es de un euro… pero la otra sí puede serlo.
Respuesta 2. El día en el que se adelante la hora en primavera para adaptarse al horario de verano, puesto que es el día del año que menos horas tiene.
Respuesta 3. 11. Pongámonos en el peor de los casos, en el que Juan coge los diez guantes derechos (o izquierdos) de ambos colores, lo que le haría imposible obtener una pareja. Con uno más le bastaría para completar la pareja.
Respuesta 4. Tan sólo una, puesto que en las ocasiones consecutivas estaríamos restándolo al número 1.110, 1.109, 1.108…
Respuesta 5. Su madre.
Respuesta 6. En segundo lugar.
Respuesta 7. Cayendo desde el primer piso: el enunciado no identifica de dónde cae la persona.
Respuesta 8. El loro es sordo.
Respuesta 9. ¿De qué color son tus ojos?
Respuesta 10. Seguirá teniendo 20. Llamarlos de otra manera no provoca que se transformen.
Si se ha quedado con ganas de más, intente resolver el acertijo que los chinos ponen a los niños de 6 años
Tomado de:
El Confidencial
¿Cuántas has contestado correctamente (sin hacer trampas y mirar la respuesta)?
- El padre de Juan le dice a su hijo que le va a otorgar dos monedas de curso legal. “Entre las dos suman tres euros, pero una de ellas no es de un euro”. ¿Cuáles son las monedas?
- ¿Qué día del año hablan menos los charlatanes?
- Juan se levanta por la mañana y descubre que la luz de la habitación no funciona. Abre el cajón de los guantes, en el que hay diez guantes negros y diez azul oscuro. ¿Cuántos debe coger para asegurarse de que obtiene un par del mismo color?
- ¿Cuántas veces puede restarse el número 1 del número 1.111?
- Dos personas viajan en coche. La menor es hija de la mayor, pero la mayor no es su padre. ¿Quién es?
- En una carrera, un corredor adelanta al que va segundo. ¿En qué posición se coloca?
- ¿Cómo puede sobrevivir alguien que cae de un edificio de 50 pisos?
- Una mujer compra en una tienda de animales a un loro que, según le promete el dependiente, es capaz de repetir todo lo que oiga. Y, sin embargo, la mujer devuelve al animal una semana después puesto que no ha pronunciado ni un solo sonido, a pesar de que le ha hablado continuamente. Sin embargo, el dependiente no la ha engañado. ¿Qué ha pasado?
- Conduces un autobús, en el que se montan 18 personas. En la siguiente parada, se bajan 5 pero suben otras 13. Al llegar a la siguiente estación, se bajan 21 y se suben otras 4. ¿De qué color son los ojos del conductor?
- Un granjero tiene 10 conejos, 20 caballos y 40 cerdos. Si llamamos “caballos” a los “cerdos”, ¿cuántos caballos tendrá?
RESPUESTAS
Respuesta 1. Una de dos euros y otra de un euro. El padre de Juan le dice a su hijo que una de ellas no es de un euro… pero la otra sí puede serlo.
Respuesta 2. El día en el que se adelante la hora en primavera para adaptarse al horario de verano, puesto que es el día del año que menos horas tiene.
Respuesta 3. 11. Pongámonos en el peor de los casos, en el que Juan coge los diez guantes derechos (o izquierdos) de ambos colores, lo que le haría imposible obtener una pareja. Con uno más le bastaría para completar la pareja.
Respuesta 4. Tan sólo una, puesto que en las ocasiones consecutivas estaríamos restándolo al número 1.110, 1.109, 1.108…
Respuesta 5. Su madre.
Respuesta 6. En segundo lugar.
Respuesta 7. Cayendo desde el primer piso: el enunciado no identifica de dónde cae la persona.
Respuesta 8. El loro es sordo.
Respuesta 9. ¿De qué color son tus ojos?
Respuesta 10. Seguirá teniendo 20. Llamarlos de otra manera no provoca que se transformen.
Si se ha quedado con ganas de más, intente resolver el acertijo que los chinos ponen a los niños de 6 años
Tomado de:
El Confidencial
Problemas razonados de álgebra... sin álgebra
El problema de edades del post de las 11 preguntas de ENLACE se puede responder sin álgebra, es decir, sin manipulacones algebraicas. Este hecho me llevó a redactar el presente post, el cual puede ser de alguna utilidad para los adolescentes interesados en las matemáticas. El post presenta varios problemas razonados clásicos. Las soluciones aquí presentadas representan una curiosidad de razonamiento lógico, basado en inferencias a partir de los datos y manteniendo la simbolización a un mínimo.
1. El padre tiene 20 años más que su hijo. Dentro de 12 años tendrá el doble que su hijo. ¿Qué edad tienen?
Solución
Puesto que la diferencia de edades no cambia con los años, entonces
20 es igual a la edad del hijo más 12. Es decir, el hijo tiene 8 y el
padre 28.
2. Las edades de un matrimonio suman 62 años. Cuando se casaron,
hace 10 años, la novia tenía 3/4 de la edad del novio. ¿Qué edad
tienen?
Solución
Hace 10 años sus edades sumaban 42, lo cual es equivalente a 7/4 de
la edad del novio. Es decir, un cuarto de la edad del novio era 6 años.
De aquí que tenían 18 y 24. Por tanto, actualmente tienen 28 y 34.
(Otra forma: si hubiesen tenido la misma edad en la boda, sería 21; por
tanteos se llega a que tenían 18 y 24, etc.)
3. Hace 6 años el padre tenía 4 veces la edad del hijo. Dentro de 10 tendrá el doble. ¿Qué edad tienen?
Solución
La diferencia de edades hace 6 años era 3 veces la edad del hijo.
Dentro de 10 esta diferencia será la edad del hijo. Pero la diferencia
es constante. Por tanto, si h era la edad del hijo hace 6 años, 3h=h+16.
Es decir, el hijo tenía 8 hace 6 (y el padre 32). Así que ahora tiene
14 y el padre 38.
4. Tres enteros consecutivos suman 204. Encuéntralos.
Solución
Si fueran iguales sería el 68. Pero son consecutivos. Por tanto son los consecutivos 67, 68, 69.
5. El perímetro de un cuadrado es el triple de otro cuyos lados miden 8 unidades menos. Calcular el lado de cada uno.
Solución
El perímetro del grande tiene 32 unidades más que el del pequeño y
es el triple que el de éste. Por tanto, p+p+32=4p. Es decir, el
perímetro del pequeño es de 16 unidades (pues 32 tiene que ser 2p). La
respuesta es entonces 4 y 12.
6. Hace 12 años el padre tenía cuatro veces la edad del hijo y
dentro de 12 su edad será solamente el doble ¿cuántos años tienen?
Solución
Hace 12 años la diferencia de edades era 3 veces la edad del hijo, y
dentro de 12 años tal diferencia será la edad del hijo. Pero la
diferencia de edades se mantiene constante. Si h es la edad del hijo
hace 12 años, se tiene 3h=h+24. Es decir, la edad del hijo hace 12 años
era de 12 y la del padre 48. Por tanto, actualmente tienen 24 y 60.
7. Tres impares consecutivos suman 81. Encuéntralos.
Solución
Si los tres fuesen el mismo sería el 27. Pero son consecutivos. Luego son 25, 27, 29.
8. Descomponer el número 48 en dos sumandos, de tal manera que
dividiendo uno entre el otro se obtenga 3 de cociente y 4 de residuo.
Solución
Si una parte entre la otra fuese 3 exacto, entonces las partes
serían 36 y 12. Pero sobran 4. Por tanteos se llega a: 37/11=3+4/11 y ya
está.
Modelo algebraico:
La condición se deja modelar como a/b=3+4/b,a+b=48 . Este sistema se resuelve fácilmente como sigue:
9. Dos números enteros consecutivos son tales que la mitad del menor más el
mayor, excede en 13 a 1/5 del menor más 1/11 del mayor. Hállalos.
Solución
Los dos números son enteros. El menor es divisible entre 10 (pues
es divisible entre 2 y entre 5). El mayor es divisible entre 11 (pues se
habla de 1/11 del mayor). Pero los números son consecutivos. Por tanto
los números son 10 y 11 (no hay otra forma de que un número terminado en
0 tenga un consecutivo –y por tanto terminado en 1-- divisible entre
11).
Modelo algebraico:
Sean m y m+1 los números. Entonces la condición se expresa como
Lo que sigue es simplificar hasta que la solución sea obvia:
Comentario general sobre los problemas
El último problema demuestra que un planteamiento algebraico
directo puede llegar a ser muy tedioso. Sin embargo, tiene la ventaja de
que su solución es casi automática --si es que se tiene la habilidad de
la manipulación algebraica y no se cometen errores. La solución sin
álgebra exige extraer conclusiones de los datos. En otras palabras, la
solución algebraica exige habilidad de manipulación algebraica, mientras
que la solución no algebraica exige razonamiento.
Por otro lado, la solución algebraica no se salva del razonamiento.
Pues en el paso inicial de planteamiento o modelación está presente una
habilidad de traducción a símbolos que no se puede hacer de manera
automática, y en la interpretación de la solución hay que regresar al
modelo inicial para darle un sentido a los resultados numéricos
obtenidos en la manipulación algebraica.
En síntesis, la manipulación algebraica de símbolos y el
razonamiento se complementan en la solución de un problema razonado (y
no son, como muchos creen, o una cosa o la otra, es decir, no son dos
opciones para elegir una de ellas). Ambas habilidades son igualmente
importantes en la resolución de problemas matemáticos.
No está de más añadir unas palabras sobre el status de los
problemas razonados. En primer lugar se debe destacar que no son una
invención reciente (como lo atestiguan los problemas del Papiro de
Rhind); en segundo lugar, deben verse como acertijos (y no como una
aplicación de las matemáticas a la vida real): la pregunta pertinente
acerca de un problema razonado no es si es realista, sino si es lo
suficientemente interesante para atraer la atención del cognizador.
Ejercicios
1. Dentro de 18 años Manolo tendrá cinco veces la edad que tenía hace dos años. ¿Qué edad tiene ahora?
2. Un tren tiene 8 vagones. Los de primera clase tienen una
capacidad de 48 pasajeros, mientras que los de segunda tienen una
capacidad de 64. Calcular el número de vagones de segunda si se sabe que
la capacidad total del tren es de 480 pasajeros.
3. El ángulo mayor de un triángulo mide 6 veces la medida del más
pequeño. El tercer ángulo mide 75 grados. ¿Cuánto miden los otros dos?
Fuente:
Suscribirse a:
Comentarios (Atom)