Matemáticas: el problema de las pinturas de Mondrian

Los cuadros geométricos de Piet Mondrian, una de los máximops representantes del arte abstracto mundial, esconden mucha matemática... y tmbién este rimpecabezas, o problema, que les traemos a continuación.

El problema matemático de Mondrian consiste en dividir una cuadrícula de dimensiones n x n, en rectángulos y cuadrados de lados enteros e incongruentes entre sí (es decir, que no haya dos iguales), de tal modo que la diferencia entre la superficie del rectángulo mayor y el menor sea la menor posible. Esa resta dará la puntuación.

¿Cómo dijo?

Este enunciado, formulado de esta manera, en abstracto, resulta difícil de entender, pero se ve muy fácilmente con un caso concreto.

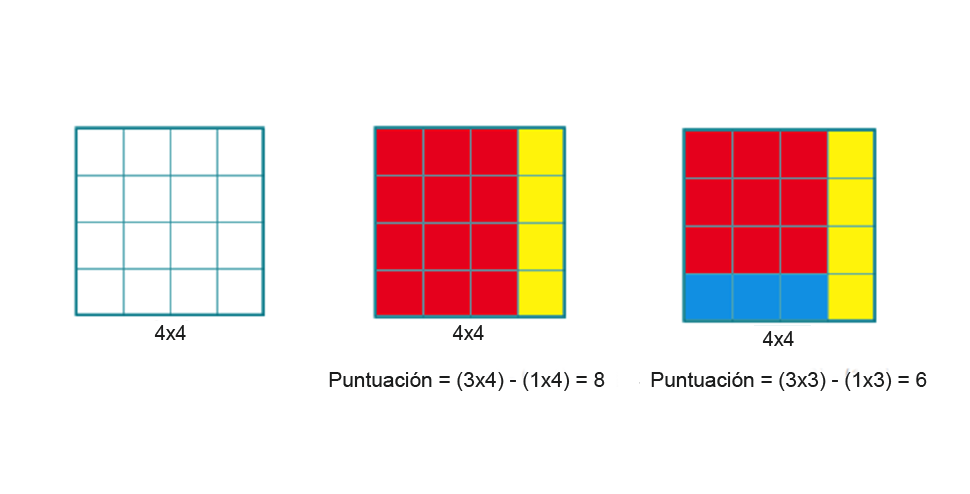
Por ejemplo, tomemos la cuadrícula de 4×4. Una posible solución es dividir el cuadro en dos rectángulos de 3×4 y 1×4, lo que otorga una puntuación de 8. Una forma de mejorar el resultado es dividir la cuadrícula en 3 rectángulos, lo que permite rebajar la puntuación a 6.

Pasatiempo N° 01:

Todavía hay una solución mejor para una cuadro 4×4, una distribución óptima que arroja una puntuación de 4. ¿Cuál es? Busca la respuesta.

Fue a partir de 1915, luego de haber estudiado a profundiad los principios de movimientos como el impresionismo, el expresionismo o el cubismo, cuando Piet Mondrian comenzó a pintar sus famosos cuadros. Estas obras sublimaban la abstracción y simplificación de las formas hasta limitar los elementos a líneas rectas y rectángulos; y los colores empleados a los primarios (rojo, amarillo y azul) y los acromáticos (gris, blanco y negro). Con este lenguaje, el pintor trataba de reflejar el equilibrio de opuestos —líneas vs superficies; formas horizontales vs verticales; colores vivos vs ausencia de color— que gobernaban la naturaleza y el universo entero y que constituía su esencia y espíritu... ¡bastante profundo y ambicioso! ¿verdad?

Ahora vamos a dar un paso más, pasemos a la siguiente cuadrícula:

Pasatiempo 2:

Aquí se muestra la mejor solución para el caso de un cuadro de 5×5, que permite una Puntuación de 4.

En el caso de un cuadro de 6×6, la mínima puntuación posible es 5, ¿cuál es la solución que permite alcanzar este valor?

¿Y cuál es la solución óptima para un cuadro de 8×8?

 

Pero aquí no acaba todo, el problema se vuelve más complejo y desafiante, sigue leyendo AQUÍ. 

Por qué enganchan los videojuegos

• Millones de personas en todo el mundo están enganchadas a juegos como Apalabrados, Farmville, Angry birds, Tetris o Buscaminas. Aprovechan un hueco en su agenda personal o laboral para una partidita y se descubren una hora después todavía jugando.

El gran hobby de Teresa siempre ha sido la lectura. Cualquier tiempo muerto o de espera era bueno para sacar su libro y leer unas páginas. Eso, hasta que hace dos meses descubrió Apalabrados, el videojuego que consiste en formar palabras combinando las siete letras que se proporcionan en cada baza, a imagen y semejanza del tradicional Scrabble. Ahora, mientras se cuece la verdura para la cena, mientras espera que su hijo salga de clase o ve un programa de televisión, Teresa no puede dejar de comprobar en su móvil o en su tableta cuál ha sido la última palabra puesta por su contrincante o qué posibles combinaciones tiene para cuando llegue su turno. Y si el rival se demora en la respuesta, rápidamente inicia otras partidas en busca de nuevas opciones para combinar palabras y continuar jugando. Puede revisar tres o cuatro veces en cinco minutos si ya han movido ficha los rivales. ¡Ella, a quien no gustan los videojuegos y discute con sus hijos por el abuso de la videoconsola! Es cierto que no juega todos los días, pero si empieza… Recuerda que algo similar le ocurrió hace muchos años cuando descubrió el Tetris. “¿Qué tienen esos juegos que enganchan tanto?”, se pregunta.

Los psicólogos y quienes se dedican a crear videojuegos lo tienen muy claro: lo que determina que un juego sea más o menos adictivo (entendida esta adicción como que resulta atractivo, no como enfermedad) es, fundamentalmente, su estructura y que esta active las rutas de neuronas que transmiten dopamina de una región del cerebro a otra. “Los juegos más adictivos son los que activan la zona reptil del cerebro, la más primitiva, el mecanismo de recompensa básica que tenemos todos los animales superiores: si algo te hace sentir bien cuando lo haces y cuando recuerdas que lo hiciste, te animas a volver a hacerlo”, explica Carlos González Tardón, psicólogo especializado en videojuegos.

El director del máster en Creación de Videojuegos de la Universitat Pompeu Fabra y director de Novorama Technology, Daniel Sánchez-Crespo, enfatiza que los videojuegos estimulan los circuitos del aprendizaje, y el cerebro humano está diseñado para segregar neurotransmisores, como la dopamina, para recompensarnos cuando aprendemos algo. “Cuando dos perros se pelean de broma, sonríen porque su cerebro los recompensa una actividad que supone un aprendizaje, un entrenamiento válido para su supervivencia; cuando un niño salta a la comba se ríe porque su cerebro le está gratificando algo que le hace ganar agilidad; y lo mismo ocurre cuando juegas a un videojuego que ejercita tu mente resolviendo o previniendo problemas: el cerebro te recompensa con dopamina” y eso te hace sentir bien y querer repetirlo. Y añade que, cuanto más aprendizaje conlleve el juego, cuantas más decisiones hayas de tomar y más rápidamente, más ejercitas el cerebro, más estimulante resulta y más engancha. “El Tetris resulta tan adictivo porque estás tomando muchas decisiones en muy poco tiempo y eso al cerebro le gusta mucho, como ocurre también con otros juegos de plataforma, como el popular Mario, que te obliga a una gran gimnasia cerebral”, apunta Sánchez-Crespo.

Lea el artículo completo en:

La Vanguadia

Juegos de lógica: Armando rascacielos

Skyscrapers es una especie de Sudoku en el que las pistas están fuera del tablero. Hay que imaginar que la matriz es como una ciudad, y en cada casilla hay un rascacielos de cierta altura: la flecha indica cuántos rascacielos se ven en línea recta desde esa posición teniendo en cuenta que los más altos no dejan ver a los más pequeños. Aparte de eso no pueden repetirse los números en las filas o columnas.


Cada problema puede resolverse usando pura lógica. Explicado así parece fácil, y de hecho los primeros módulos son fáciles, pero cuando la matriz aumenta de tamaño y las pistas son más complicadas el asunto deja de ser trivial.

Tomado de:

Microsiervos