27 de septiembre de 2012
Los Supersónicos: 50 años de optimista retrofuturismo
24 de septiembre de 2012
El alucinante 'anime' amateur de 'Star Wars'
¿Harto de los despropósitos de Lucasfilm? Un fan de la saga galáctica ha recreado un duelo espacial entre el Imperio y la Alianza al estilo nipón. Aviso: ¡El video està bacàn!.
Por CINEMANÍA.
¿Qué es la temperatura? Una explicación a través de animaciones
Dentro del caos y la aleatoriedad más absolutos podemos encontrar uno de los más sencillos y elegantes modelos matemáticos jamás construido en la historia de la física teórica. Hoy analizaremos la solución el enorme reto al que se enfrentaba la física de finales del siglo XIX: explicar qué cosa era eso que llamamos temperatura. Espero que os resulte amena esta introducción con animaciones y simulaciones, de las aprovecho para liberar el código fuente.
1. Jugando al billar
 |
| Esta preciosa puesta de sol, fotografiada desde la estación espacial ISS, revela perfectamente los pocos kilómetros de atmósfera que nos envuelven (fuente). |
 |
| Choque perfectamente elástico de dos esferas ideales. |
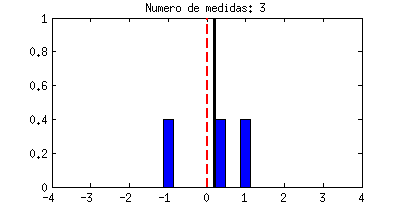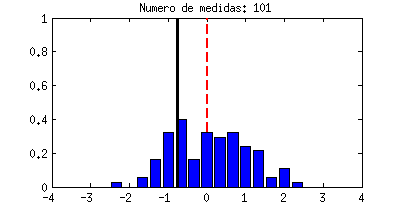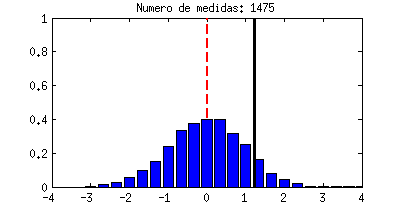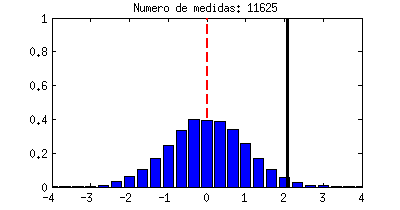 |
| Ejemplo de una variable aleatoria con distribución Gaussiana. |
14 de marzo de 2012
Video: La ajetreada evolución de la Luna desde su formación hasta hoy
Si eres de los que en las noches mira al cielo y se queda horas pegado observando la Luna y más de alguna vez se ha preguntado por qué tiene distintas tonalidades si no hay nada y cómo se fueron creando, entonces este video con su completa evolución -desde su forma original, hace 4.500 millones de años- es para ti.
Describe y muestra el impacto con el otro satélite que orbitaba alrededor de la Tierra y que formó la Cuenca Aitken en el Polo Sur lunar, hace unos 4.300 millones de años. Luego pasa por el período de fuerte bombardeo de meteoritos (hace entre 4.100 a 3.800 millones de años) que formó su cuenca principal, el cual -a su vez- fue seguido de otro lapso en que debió soportar una tormenta de muy larga duración (más de 2.000 millones de años, aunque con asteroides de menor tamaño).
Finalmente, hace cerca de 1.000 millones de años, una nueva serie de impactos que generaron los denominados cráteres rayo, dio la forma y aspecto definitivo que conocemos en la actualidad.
Pero mejor me callo y les dejo ver la animación realizada por un equipo de científicos del Centro de vuelo espacial Goddard de la NASA, conformado por información obtenida de la sonda Lunar Reconnaissance Orbiter:
Fuente:
FayerWayer
30 de noviembre de 2011
La Historia Universal en 3 minutos 30 segundos
Kalle Mattson - Thick As Thieves (Official Video) from Kevin Parry on Vimeo.
La Historia de nuestro planeta es algo difícil de resumir, aunque en la cabecera de entrada de The Big Bang Theory se resuma rápidamente: la formación de la Tierra, la era de los dinosaurios, los primeros homínidos, el antiguo Egipto, el Imperio Romano, la Edad Media y, dando un gran salto, la carrera espacial entre Estados Unidos y la Antigua Unión Sovética. Millones de años de historia que ocupan volúmenes de libros en grandes bibliotecas y que, realmente, es complicado sintetizar. Un grupo de diseñadores y animadores decidió resumir toda la historia de la Tierra (y avanzar algo de su futuro) en un bello proyecto de animación de 3 minutos 30 segundos.
El equipo de 6 personas, formado por Kalle Mattson como guionista, Kevin Parry como animador y director del cortometraje, Carla Veldman como diseñadora y animadora, Andrew Wilson como diseñador y Andrea Nesbitt como especialista en vídeo, dedicaron 6 meses de trabajo a este proyecto de animación bajo stop-motion en que el recrearon la historia del mundo (con un sorprendente y geek final sobre su futuro) utilizando un escenario de fieltro y unas figuras de papel.
Tomado de:
1 de agosto de 2011
Futurama y las matemáticas
Como en algunas otras series (como los simpsons) y películas, en futurama aparecen algunos detalles que sobre todo si no estamos familiarizados con el mundo de las matemáticas y de la física se nos pueden pasar por alto o podemos no entender a lo que se refieren.
- En el capítulo Yo, compañero de piso el número de la habitación de Bender es 00100100 que es 36 en binario y capicúa. Además en el código ASCII el 36 equivale al símbolo del dólar ($). En el edificio de Bender hay 256 habitaciones (desde la 00000000 hasta la 11111111) exactamente las mismas que símbolos tiene el código ASCII.

- En el capítulo El bocinazo aparece reflejado en el espejo el número 1010011010 que es el número 666 en binario.


- La descongelación de Fry:
- En varios capítulos aparece el número 1729:
- En el capítulo Unos valiosos pececitos los intereses que le dan a Fry son más o menos correctos:
Dinero final = 0.93 * (1.0225)^1000 ya que a cada año que pasa, el saldo de la cuenta se va multiplicando por 1.0225. Se obtienen 4.283.508.449 dólares y 71 centavos.
- En el capítulo El infie rno está en los demás Robots nos muestran algunos edificios con forma geométrica curiosa el "Madison Cube Garden" y el Hotel "Trump Trapezoid"

- Flexo y Bender tienen su número de serie relacionado:
Flexo: 3370318 = 1193 + 1193
Bender: 2716057 = 9523 + (-951)3
Además, esta descomposición es única.
- El cine que aparece en los capítulos Bender salvaje y Salí con una robot se llama "Loew's ℵ0-Plex"

- En el capítulo Un clon propio el club que diseña el profesor Farnsworth en su juventud se llama "Schrödinger's Kit Kat Club", que puede traducirse como "Club de Gatitas de Schrödinger"
- En el capítulo Mi problema con los Poppler en la publicidad de los Popplers de Fishy Joe's se lleva la cuenta del número de Popplers servidos, y en este caso es de 3.8 x 1010 que es la distancia media entre la tierra y la Luna. Esto quiere decir que si un Poppler midiese 2 cm. y los pusiéramos a todos en fila, podríamos ir a la Luna y volver, lo que podría ser el motivo de un slogan promocional del estilo: "¡Hemos vendido tantos popplers como para ir a la Luna y volver!". La cifra final de Popplers servidos (mencionada por Kif) es de 198 billones americanos, es decir 1.98 x 1011 (teniendo en cuenta que 1 billón americano = mil millones europeos), más de cinco veces la anterior.
- En el capítulo La ruta de todo mal el envase de la botella de Klein es la versión en R3 de la botella de Klein(una superficie no orientable en R4).

Otras marcas de cerveza que aparecen son "Olde Fortran" y "St. Pauli's Exclusion Principle Girl". La primera hace referencia al lenguaje de programación Fortran y la segunda es una parodia de la cerveza ya existente "St. Pauli", es un juego de palabras con el principio de exclusión de Pauli.
Fuente:
El Universo de Wanders
8 de julio de 2011
Para entender al Pato Donald... ¡y a Pitágoras!

Las cosas ya se hacían bien en la década de los 50. El cortometraje que veis sobre estas líneas, “Donald in Mathmagic Land” (título original), me sedujo por completo una vez que fui padre, pues no recuerdo haberlo visto en TVE cuando era niño (pero aquí en Perú si se vió, lo pasaron varias veces a fines d elos setenta e inicios de los ochentas por América Televisión). El corto data de 1959, fue dirigido para la Disney por Hamilton Luske, quien se apoyó en el conocimiento del físico alemán Heinz Haber, empleado como experto científico. Haber, otro caso de alemán emigrado a Estados Unidos tras la segunda guerra mundial, como su amigo Wernher von Braun, había ya colaborado con Disney en sus películas sobre el espacio, y dos años después ayudaría también a crear el estupendo corto “Our friend the atom” (que puede encontrarse subtitulado al castellano en Youtube).
La animación fue nominada por la Academia Cinematográfica para el Oscar al mejor corto documental, y en la década de los 60 se entregaron copias en las escuelas de todos los Estados Unidos, por lo que se convirtió en uno de los recursos educativos más populares jamás creados por la factoría Disney; y al mismo tiempo una inteligente y extensa campaña de marketing para el pato de Disney.
Más de medio siglo después sigue manteniendo un gran valor didáctico pese a la evidente pérdida de frescura. Ahora que los niños estarán de vacaciones por Fiestas Patrias y disponen de mucho tiempo libre (a menudo malgastado frente al televisor) es un buen momento para que tus hijos descubran que el pato Donald también puede ser un divertido profesor de matemáticas.
La información sobre el corto la encontré en Wikipedia (inglés).
Donald en el país de la matemáticas from angel on Vimeo.
Fuente:
Si usted es docente o padre de familia:Actividades matemáticas con Donald (pdf)
26 de junio de 2011
El Origen de las Especies: La serie animada
Hoy se ha puesto en contacto con El ojo de Darwin el director de animación Bob Etchingham para presentarnos el trailer de su nuevo e interesantísimo proyecto titulado “Origin of Species – The Animated Series“.
De momento no tenemos demasiados detalles sobre esta producción, pero se trata de un proyecto que pretende llevar el conocimiento científico sobre la evolución a los niños de una forma que resulte interesante y educativa. “The aim of the series is to educate children in an interesting and informative way about evolution.” nos cuenta Bob Etchingham.
Esperaremos ansiosos el estreno de la serie.
Tomado de:
El Ojo de Darwin



