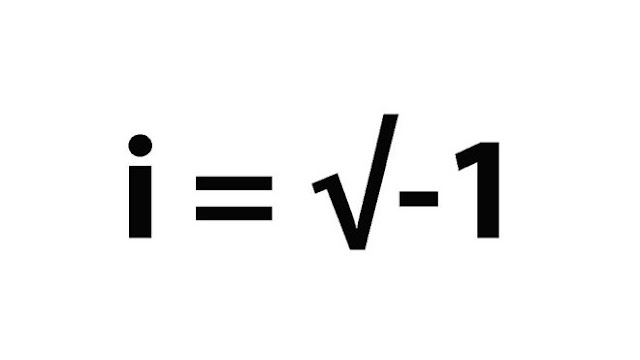¿Qué son los números imaginarios?

En la Italia renacentista de comienzos del siglo XVI uno de los espectáculos callejeros más populares en la ciudad universitaria de Bolonia eran los duelos. Pero no solo los de espadas. También había combates puramente intelectuales.

Se trataba de desafíos matemáticos, en los que dos o más expertos batallaban por encontrar la solución a un problema. El duelo se llevaba a cabo en plazas públicas y era seguido por miles de habitantes.

Fue en esta época que algunos matemáticos italianos se empezaron a dar cuenta de que algunas ecuaciones eran imposibles de resolver. 

En particular, aquellas cuya resolución requería calcular la raíz cuadrada de números negativos.
Como quizás recuerdes de la escuela, los números negativos no tienen raíces cuadradas: no hay un número que, cuando se multiplica por sí mismo, da un número negativo. 
 
Esto se debe a que los números negativos, cuando son multiplicados, siempre producen un resultado positivo. Por ejemplo: -2 × -2 = 4 (no -4).

Pero los matemáticos Niccolo Fontana (alias Tartaglia) y Gerolamo Cardano se dieron cuenta de que si permitían la existencia de raíces cuadradas negativas, podían resolver ecuaciones verdaderas -o con "números reales", como se conoce a los números que poseen una expresión decimal-.

La "unidad imaginaria" o "i" es la raíz cuadrada de -1, un número que fue inventado en el siglo XVI en Italia. >

Fue así como crearon una unidad nueva, imaginando la raíz cuadrada de -1 (o √-1 en términos matemáticos).

En 1573 otro matemático renacentista, Rafael Bombelli, explicó cómo funcionaba la aritmética con este nuevo concepto, en una obra llamada "Álgebra".

Allí señaló que la unidad nueva no era positiva ni negativa y, por lo tanto, no obedecía las reglas habituales de la aritmética.

Por cerca de un siglo muchos pensadores rechazaron esta nueva idea, llamando a esta unidad inventada "ficticia, imposible o sin sentido".

Uno de los detractores fue el filósofo francés René Descartes, quien en su obra "La Géométrie" (1637) bautizaría a la invención con el término despectivo de "números imaginarios".

i

Pasarían muchas décadas más para que los matemáticos empezaran a aceptar a estos números imaginarios, que desafiaban la lógica, como algo válido y genuino.

En 1707, otro francés, Abraham de Moivre, relacionó los números imaginarios con la geometría, logrando así usar esta disciplina para resolver complejos problemas algebraicos.

Setenta años más tarde, los números imaginarios tendrían finalmente su propio símbolo: i (gracias al matemático suizo Leonhard Euler).

Y su uso permitiría extender el sistema de números reales (R) al sistema de números complejos (C), donde se combinan números reales con números imaginarios.

Quizás todo esto suena como algo completamente abstracto y sin utilidad real, que solo podría interesarle a intelectuales que viven en el mundo de las ideas, pero esa está lejos de la realidad.

En el siglo XX, los números imaginarios empezaron a tener muchos usos prácticos, permitiendo a ingenieros y físicos, entre otros, resolver problemas que de otra forma no hubieran tenido solución.

Telecomunicaciones

Hoy estos números imaginarios y complejos están detrás de algunas de las tecnologías más esenciales que usamos.

Resultaron especialmente valiosos cuando se inventó la electricidad, ya que son muy útiles para analizar cualquier cosa que se expresa en ondas (como las ondas eléctricas).
La ingeniería eléctrica utiliza números complejos, en los que "i" es usado para indicar la amplitud y la fase de una oscilación eléctrica.


Sin estos números, no se hubiera podido desarrollar las telecomunicaciones. No existiría la radio, la televisión e internet y hoy no estarías leyendo esta nota en tu computadora, tablet o celular.
Los números imaginarios también permitieron todo tipo de desarrollos tecnológicos y científicos, desde el radar y el GPS hasta la resonancia magnética y las neurociencias.

La física cuántica reduce todas las partículas a formas de onda, lo que significa que los números complejos son fundamentales para comprender ese extraño mundo.

No sólo podrían ser clave para el futuro, sino que algunos creen que eventualmente podrían servir para responder una de las grandes incógnitas que siguen dejando perplejos a los científicos: ¿qué pasó antes del Big Bang y cuándo empezó realmente el tiempo?

¿En serio?

La clásica teoría general de la relatividad de Albert Einstein vinculó el tiempo con las tres dimensiones espaciales con las que todos estamos familiarizados (arriba-abajo, izquierda-derecha y adentro-afuera), creando un "espacio-tiempo" cuatridimensional en el que el tiempo solo puede avanzar. 

Una teoría brillante, pero cuando se aplica a la creación del Universo surgen problemas.
Pero si invocas la teoría cuántica y le agregas algo de tiempo imaginario y todo empieza a cobrar sentido... al menos para los cosmólogos. 

El tiempo imaginario se mide en números imaginarios y, a diferencia del tiempo real, puede avanzar y retroceder como una dimensión espacial adicional.
Y eso le da al Big Bang un momento para comenzar.

Fuente: BBC Mundo

Cambiando la regla y el compás por piezas de mecano para construir distintos tipos de números

Se acerca el período navideño y con él la tradicional costumbre de los regalos. Aunque es posible que actualmente ya no sea tan popular, en otra época el mecano era uno de los juegos estrella en las cartas que los niños enviaban a los Reyes Magos. Todos hemos jugado alguna vez con este popular juego que consiste en ensamblar tiras metálicas mediante tornillos y tuercas.

Combinando estas tiras se pueden conseguir formas y mecanismos muy diversos, desde simples figuras a complejas y elaboradas construcciones.

  Tiras de Mecano, junto a otros tipos de piezas (imagen tomada de aquí.)
Pero aquí hablamos de matemáticas, y eso es lo que vamos a hacer. Vamos a explorar una faceta muy diferente y menos conocida de este juego de construcción muy relacionada con las matemáticas.

En este blog hemos hablado en bastantes ocasiones sobre las construcciones con regla y compás (por ejemplo en I, II, III, IV, V y VI). Bien, pues lo que vamos a hacer en esta entrada es cambiar la regla y el compás por piezas de mecano. Es decir, vamos a analizar qué tipo de construcciones relacionadas con regla y compás pueden realizarse con las tiras metálicas de un mecano. Por ejemplo, ¿qué números se pueden construir? ¿Podremos construir un polígono regular? ¿Y bisecar un ángulo? ¿Y trisecarlo? No perdáis detalle, nos esperan muchas sorpresas relacionadas con este tema en lo que será una serie de artículos dedicados al mismo.

Antes de nada vamos a introducir algunas cuestiones relacionadas con las piezas que vamos a utilizar y la manera que vamos a tener de trabajar. Como hemos dicho, usaremos solamente las tiras típicas del mecano, que constan de un cierto número de agujeros, donde consideraremos que están situados números enteros, y que se pueden unir unas con otras mediante un tornillo.

Supondremos que estas piezas solamente no tienen dos dimensiones, por lo que para nosotros tendrán altura cero, para no tener problemas a la hora de poner varias piezas unidas en el mismo agujero. Evidentemente esto no es verdad en el mundo real, y por eso mismo las construcciones más elegantes serán las que eviten esta circunstancia.

Construcción de los números racionales

Las tiras, como hemos dicho, tienen una longitud entera, ya que los agujeros están espaciados una cantidad entera. Aunque esto en principio podría parecer una restricción, en realidad no es así. Podemos construir fácilmente otras tiras de longitud racional (no entera). Así como los números racionales surgen como extensión de los números enteros para expresar cantidades de la forma , con .

Para lograrlo, solamente hay que utilizar la semejanza de triángulos. Como se puede observar en la figura siguiente, podemos crear una tira de longitud racional . Ya que y pueden elegirse libremente, podemos crear cualquier número racional sin limitación.

Lea el artículo completo en:

Gaussianos