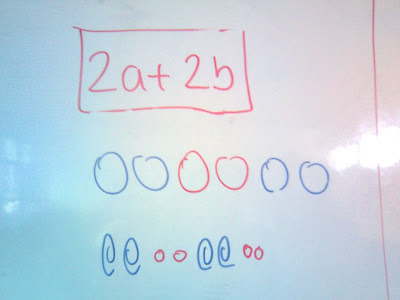Método Singapur para razonar problemas verbales elementales

Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con

Un ejemplo

Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?

Solución algebraica

Sea x la cantidad recibida de su madre. Entonces, el problema se modela de la siguiente manera: 7+x=2(2+x). Es decir, x=3 --recibieron 3 pesos de su madre.

Elemental ¿no es cierto? Pues sí pero no para un niño de quinto año (11 años). Y ello porque no hay álgebra en aula de primaria. (No se le puede enseñar porque aún no alcanza la etapa de pensamiento formal en su desarrollo cognitivo --según se sabe.)

En la escuela primaria se prepara a los alumnos en aritmética, y se esperaría que la forma de enseñarla los prepare para el álgebra, la cual tiene que esperar la educación secundaria.

Y, sin embargo, el problema está al alcance de un niño de 11 años (bueno, por lo menos en teoría). Por ejemplo, lo puede resolver por tanteos: se propone al cantidad recibida y se verifica si cumple la condición del "doble que". Pero ese método tampoco es enseñado, pues se cree que es un método natural de resolverlo.

Otra forma de resolverlo es diagramático --el cual sí se enseña en Singapur. Sería más o menos como sigue:

Los datos del enunciado se representan gráficamente (la representación gráfica ayuda al razonamiento).

Se agrega al diagrama la cantidad recibida --la cual no se sabe cuánto es pero... Una vez teniendo el diagrama ya se puede razonar sobre él. Y se puede usar el método del "número escondido": la cantidad recibida más 2 es 5, por tanto la cantidad recibida es 3.

Entre lo concreto y lo abstracto está el diagrama

Todo mundo está de acuerdo en que, en el desarrollo cognitivo de los niños, primero es lo concreto y después lo abstracto. Pero intermedio entre esas dos formas de razonar está el razonamiento diagramático. Y el método Singapur de resolución de problemas razonados le apostó a esa hipótesis (clásica pero poco apreciada). El lema del currículum de la educación matemática básica en Singapur refleja esa apuesta: concreto, pictórico, abstracto.

Nota geográfica y económica: Singapur es un pequeño país en el extremo sur de la península de Malasia, sin ser parte de ésta pues es una isla --de hecho son varias islas. Añadiré que, de acuerdo a su economía, es uno de los "cuatro tigres asiáticos" --siendo los otros tres Korea del Sur, Hong Kong y Taiwan.

Ilustración del razonamiento diagramático

Ya en otra ocasión había escrito un post sobre razonamiento diagramático y el método Singapur

En esta ocasión voy continuar ese post, ilustrando el método diagramático de Singapur con algunos problemas razonados. Voy a resolver el más difícil y los restantes se quedan como un ejercicio para el lector.

Problema 1 (edades desfasadas): Beto tiene el doble de la edad que Sandra tenía cuando Beto tenía la edad que ahora tiene Sandra. Cuando Sandra tenga la edad que ahora tiene Beto, la suma de sus edades será 45 años. Calcular la edad de Sandra.

Solución diagramática

(Hay que saber que la diferencia de edades se mantiene constante en el tiempo.) Sea d la diferencia de edades y representemos con b la edad de Beto y con s la edad de Sandra.

Desplazando las edades de Sandra y Beto d años hacia el pasado, se hace evidente que Beto tiene 4d años.

Desplazando las edades d unidades hacia el futuro, se puede ver que 5d+4d=45. Es decir, d=5. Por tanto, Beto tiene 20 y Sandra 15.

Problema 2 (suma y diferencia): Las edades de Beto y Sandra suman 35 años, y su diferencia es 5. Calcularlas.

Problema 3 (la mula y el burro): Le dice el burro a la mula "si me ayudaras con 10 ladrillos llevaríamos la misma carga". Y la mula le contesta "si tú me ayudaras con 10 llevarías el doble que yo." Calcular los ladrillos que lleva cada uno.

Problema 4 (Padre e hijo): El padre es 45 años mayor que su hijo. En 6 años éste tendrá la cuarta parte de la edad de su padre.

Problema 5. Dos números suman 60, y el mayor es cuatro veces el menor.

Problema 6. Alex tiene 48 pesos más que Arturo y éste la séptima parte de loque Alex tiene. 

Tomado de:

Mate Tam

Razonamiento diagramático en problemas de factorización

En este post voy a comentar sobre el método de reagrupamiento para factorizar una ecuación cuadrática y su correspondiente solución diagramática. Ilustro con un caso particular de toda

Una familia de problemas cuadráticos

En una ecuación cuadrática, si se puede factorizar entonces se puede representar como rectángulo --con uno de sus factores la base y el otro la altura.

Consideremos el problema de factorizar la ecuación cuadrática

ax2+(a+b)x+b=0

(donde a,b son enteros positivos).
Este problema es, en realidad, toda una familia de problemas, uno para cada par de números enteros positivos a,b. Por ejemplo, si a=2011,b=1, se tiene el problema 1A del concurso estatal OMM Tamaulipas 2012 

Por esa razón, puede ser de alguna utilidad como generador de problemas cuadráticos para los profesores de matemáticas de bachillerato. Discutamos ahora su

Solución

El método de reagrupamiento nos lleva a la siguiente ecuación equivalente:

ax2+ax+bx+b=0

Y se logra ver que es posible factorizar la ecuación como

ax(x+1)+b(x+1)=(ax+b)(x+1)=0

Y esa factorización se puede representar como un rectángulo de base x+b y altura x+1
(Nota: por el teorema del residuo, es también relativamente fácil darse cuenta que x=−1 satisface la ecuación --y lo que sigue es dividir entre x+1 para obtener el otro factor.)

Discusión

La pregunta ahora es ¿es posible factorizar una cuadrática de manera diagramática? Y, bueno, uno podría decir: sí, si es de la forma antes mencionada.

Y ¿cómo se reconoce una ecuación de la forma antes mencionada? Bueno, debería ser claro que el truco es que todos sus coeficientes sean positivos y que la diferencia entre el coeficiente de la x y el de la x2 sea igual al término independiente.

Consideremos el caso de la ecuación 5x2+7x+2. Es claro que esta ecuación satisface los dos requisitos mencionados. Y, bueno, uno entonces podría explicar a sus estudiantes:

Vean que si tomamos este rectángulo de base 5x y altura x su área es 5x2. Pero como 7x=5x+2x entonces agregando este otro rectángulo de base 5x y altura 1, y este otro --a la derecha-- de base 2 y altura x, ya tenemos el segundo término representado en estos rectángulos. Y como este otro rectángulo de la esquina arriba a la derecha es de base 2 y altura 1, entonces ya tenemos el término independiente. ¿OK? Y ahora ¿cuáles son las dimensiones de este rectángulo que hemos formado con los términos de la ecuación cuadrática? Piénsenlo un rato y me lo dicen. Etcétera, etcétera.

Esta exposición didáctica de la factorización de este tipo de ecuaciones cuadráticas es efectista. De hecho no aporta nada que no esté ya en el método de reagrupamiento.

Pero tiene la ventaja --posiblemente-- de dejar al aprendiz intrigado, y posiblemente asombrado... (se preguntará acaso sobre la forma en que los términos se acomodaron tan perfectamente en un rectángulo). Y si llega a descubrir el truco entonces la exposición fue un éxito. (Claramente, para el indiferente cualquier tipo de exposición es igualmente aburrida...)

Los saluda
jmd

Tomado de:

Mate Tam

Con Danica McKellar ¡las matemáticas también son sexys!

“Saber matemáticas es la puerta de entrada a una serie de carreras universitarias increíbles que las estudiantes nunca han considerado.” Danica McKellar se refiere a las carreras STEM, acrónimo en inglés de Science, Technology, Engineering & Mathematics (Ciencia, Técnica, Ingeniería y Matemáticas). Famosa actriz de televisión (para quienes tienen más de 30 años) por ser Winnie Cooper en la serie “Aquellos maravillosos años” (1988–1993), ha escrito cuatro libros para tratar que las chicas adolescentes sepan que ser sexy y saber matemáticas no son cosas que estén reñidas. Sus libros son bestsellers (según el New York Times). ¿Cuándo se traducirán/adaptarán estos libros al español? Quizás conviene recordarlo, aunque ya lo conté en “Matemáticas para jovencitas de la mano de una actriz de televisión,” LCMF, 02 Nov 2008.

Las mujeres son mayoría en todos los niveles de enseñanza, sin embargo, están infrarrepresentadas en los estudios científico-tecnológicos. En relación al aprendizaje de las matemáticas son muchos los factores que influyen en las diferencias que se detectan entre varones y mujeres, como  las creencias y concepciones previas, la motivación, la auto-confianza para trabajar en Matemáticas y otros aspectos afectivos. Estas diferencias de género en las actitudes hacia las matemáticas en la enseñanza obligatoria (más en secundaria y bachillerato que en primaria) han sido muy estudiadas, pero que yo sepa no existe una fórmula magistral que las resuelva.

Por ello, todas las iniciativas que busquen acercar las matemáticas a las adolescentes me parecen muy interesantes y acertadas. Danica McKellar nos ofrece un buen listado de problemas matemáticos elementales relacionados con los interesados de las adolescentes, que en muchos casos difieren de los de los adolescentes. Habrá muchas chicas interesada en el fútbol y en los coches, pero la mayoría consideran que estos temas “no son de chicas.” Reescribir los libros de texto para poner en pie de igualdad los intereses adolescentes de chicas y chicos en los problemas de materias científico-tecnológicas puede ser un camino a explorar a la hora de corregir las diferencias de género.

Fuente:

La ciencia de la Mula Francis

Cauchy y el rigor en el análisis matemático

Muchos historiadores de la matemática afirman que el rigor en matemáticas nació con Augustin-Louis Cauchy. Todo un revolucionario, Cauchy trató de establecer una base rigurosa para el análisis matemático. Un buen ejemplo fue su demostración del teorema del valor intermedio, que afirma que toda función real f(x) continua en un intervalo [a,b] asume cada valor posible entre f(a) y f(b) en ese intervalo. Parece obvio gracias a la idea intuitiva de continuidad y de hecho hasta Cauchy nadie pensó que fuera necesario demostrarlo, pero hoy en día todos los estudiantes de matemáticas se pelean con su demostración rigurosa (aunque sin saberlo, como homenaje en memoria de Cauchy). Por cierto, Cauchy enseñó la demostración de este teorema por primera vez en el curso que impartió en la École Royale Polytechnique en 1816. Su libro de texto de 1821, admirado por más de una generación de matemáticos, presenta dos demostraciones diferentes; la más famosa, la que todos los estudiantes de matemáticas aprenden, fue relegada a un apéndice. Nos lo recuerda Michael J. Barany, “Stuck in the Middle: Cauchy’s Intermediate Value Theorem and the History of Analytic Rigor,” Notices of the AMS 60: 1334-1338, Nov. 2013.


La Revolución Francesa, bajo las consignas de libertad, igualdad y fraternidad, fue acompañada de una revolución matemática. Por primera vez, la élite de los ingenieros militares y civiles comenzó a recibir una formación matemática en París que comprendía las matemáticas más avanzadas del momento. Estos ingenieros aplicaron las matemáticas que estudiaron a los problemas más acuciantes del mundo moderno: infraestructuras, la navegación, la minería, la energía e incluso a la guerra. El buque insignia de esta revolución fue la École Polytechnique (que fue rebautizada como École Royale Polytechnique tras la derrota de Napoleón y el regreso de la monarquía). En esta institución Cauchy dejó su huella como estudiante y como profesor.

Cauchy fue un profesor impopular tanto entre los estudiantes como entre sus compañeros de facultad. Sus clases eran muy densas y difíciles de seguir, muchas veces prolongaba la clase más allá de su horario oficial y además realizaba continuas revisiones del temario. Para Cauchy las matemáticas del siglo XVIII eran una disciplina que había perdido el norte. Todo un siglo de innovaciones matemáticas maravillosas que habían sido logradas a costa del rigor. Matemáticos como Euler manejaban series que no eran convergentes y expresiones formales sin sentido que producían conclusiones absurdas. No estaban claros conceptos tan básicos como el de infinito, el de límite, los números imaginarios y muchos más. Cauchy admiraba la formulación axiomática de la geometría realizada por Euclides. El álgebra presentaba un estado similar, pero era considerada por los matemáticos del siglo XVIII como una herramienta, versátil, pero de poca utilidad a la hora de resolver problemas prácticos. Por el contrario, el análisis era muy útil en todo tipo de problemas prácticos, pero carecía de un formulación rigurosa. Cauchy quería que el status de la geometría y del álgebra fuera extendido al análisis. Por ello decidió revisar todo el análisis desde el punto de vista de la geometría y apoyado por el álgebra como herramienta.

Por supuesto, el “Curso de Análisis” de Cauchy, como suele ocurrir con todo trabajo pionero, carece de rigor en muchos aspectos. Por ejemplo, Cauchy asume que todas las funciones continuas son diferenciables. Sin embargo, lo importante del proyecto de reforma del análisis iniciado por Cauchy, que trata de llevar el rigor al análisis de la mano de la geometría y del álgebra, es que inició un camino hacia el rigor cuya culminación fue el motor de gran parte de la matemática de todo el siglo XIX, con la honrosa excepción del genial Henri Poincaré que vio en el rigor un corsé del que había que deshacerse.

El cénit del rigor en las matemáticas llegó en el siglo XX con Nicolas Bourbaki, el nombre colectivo de un grupo de matemáticos franceses que, en los años 1930, se pusieron a revisar todos los fundamentos de las matemáticas con una exigencia absoluta en el rigor tratando de combatir la corriente que había nacido con Poincaré. Matemáticos como Jean Dieudonné, André Weil, Henri Cartan, Claude Chevalley, y otros antiguos alumnos de la Escuela Normal Superior de París recogieron el guante de Cauchy e impusieron a toda la matemática el concepto de rigor matemático como definición de la labor del matemático.

Un matemático es una máquina de demostrar teoremas con absoluto rigor. La máxima revolucionaria de Bourbaki es Vive la rigueur!

Fuente:

La Ciencia de la Mula Francis

Algebra de Boole: Matemáticas del siglo XIX sin las que no funcionaría internet

Estamos inmersos en plena era digital, donde los aparatos electrónicos que funcionan, básicamente, a base de recoger ceros y unos, y tratarlos de forma lógica, haciendo cosas que hasta ahora solo eran posibles en los libros de ciencia ficción. Pero como para casi todo en ciencia, hay una base matemática: El álgebra de Boole.

Historia

George Boole, (2 de noviembre de 1815 - 8 de diciembre de 1864), fué  primer profesor de matemáticas del entonces Queen's College, Cork en Irlanda (en la actualidad la Universidad de Cork , en la biblioteca, lectura de metro complejo teatral y el Centro de Boole para la Investigación en Informática se nombran en su honor) en 1849. Pero fué antes, en 1847 cuando escribió un pequeño folleto llamado "The Mathematical Analysis of Logic" , que completo con otro libro " The Laws of Thought" publicado en 1854.

Pero esto quedó en poco más que una curiosidad matemática, hasta 1948, cuando Claude Shannon la utilizó para diseñar circuitos de conmutación eléctrica biestables, aunque ya el propio Alan Touring había utilizado este mismo álgebra de forma teórica, en su diseño de la máquina de Turing (1936). Y con ello, comenzó la era de la computación digital.

Bases

Basada en la teoría de conjuntos (Teoría de Conjuntos - Matemática Aplicada a la Ingeniería), el álgebra de Boole sirve para manejar operaciones lógicas en sistemas de numeración binarios, es decir, basados en ceros y unos. De esta manera se nos permite realizar operaciones matemáticas, como sumas, restas, multiplicaciones, divisiones u operaciones lógicas, como "no algo" ó "esto y lo otro", o "si y solamente si...", tal y como esperaríamos en cualquier sistema de lógica aristotélica. Esto nos permite utilizar tablas de decisión y diagrámas de flujo de datos en los circuitos lógicos.

Para cualquier sistema algebraico existen una serie de postulados iniciales, de aquí se pueden deducir reglas adicionales, teoremas y otras propiedades del sistema, el álgebra booleana a menudo emplea los siguientes postulados:

• Cerrado. El sistema booleano se considera cerrado con respecto a un operador binario si para cada par de valores booleanos se produce un solo resultado booleano.
• Conmutativo. Se dice que un operador binario " º " es conmutativo si A º B = B º A para todos los posibles valores de A y B.
• Asociativo. Se dice que un operador binario " º " es asociativo si (A º B) º C = A º (B º C) para todos los valores booleanos A, B, y C.
• Distributivo. Dos operadores binarios " º " y " % " son distributivos si A º (B % C) = (A º B) % (A º C) para todos los valores booleanos A, B, y C.
• 
  
• Identidad. Un valor booleano I se dice que es un elemento de identidad con respecto a un operador binario " º " si A º I = A.
• Inverso. Un valor booleano I es un elemento inverso con respecto a un operador booleano " º " si A º I = B, y B es diferente de A, es decir, B es el valor opuesto de A.

Para nuestros propósitos basaremos el álgebra booleana en el siguiente juego de operadores y valores:

• - Los dos posibles valores en el sistema booleano son cero y uno, a menudo llamaremos a éstos valores respectivamente como falso y verdadero.
• - El símbolo ·  representa la operación lógica AND. Cuando se utilicen nombres de variables de una sola letra se eliminará el símbolo ·,  por lo tanto AB representa la operación lógica AND entre las variables A y B, a esto también le llamamos el producto entre A y B.
• - El símbolo "+" representa la operación lógica OR, decimos que A+B es la operación lógica OR entre A y B, también llamada la suma de A y B.
• - El complemento lógico, negación ó NOT es un operador unitario, en éste texto utilizaremos el símbolo " ' " para denotar la negación lógica, por ejemplo, A' denota la operación lógica NOT de A.
• - Si varios operadores diferentes aparecen en una sola expresión booleana, el resultado de la expresión depende de la procedencia de los operadores, la cual es de mayor a menor, paréntesis, operador lógico NOT, operador lógico AND y operador lógico OR. Tanto el operador lógico AND como el OR son asociativos por la izquierda. Si dos operadores con la misma procedencia están adyacentes, entonces se evalúan de izquierda a derecha. El operador lógico NOT es asociativo por la derecha.
• Utilizaremos además los siguientes postulados:
• P1 El álgebra booleana es cerrada bajo las operaciones AND, OR y NOT
• P2 El elemento de identidad con respecto a ·  es uno y con respecto a +  es cero. No existe elemento de identidad para el operador NOT
• P3 Los operadores ·   y + son conmutativos.
• P4 ·   y + son distributivos uno con respecto al otro, esto es, A· (B+C) = (A·B)+(A·C) y A+ (B·C) = (A+B) ·(A+C).
• P5 Para cada valor A existe un valor A' tal que A·A' = 0 y A+A' = 1. Éste valor es el complemento lógico de A.
• P6 ·   y + son ambos asociativos, ésto es, (AB) C = A (BC) y (A+B)+C = A+ (B+C).

(Fuente - http://www.monografias.com/trabajos14/algebra-booleana/algebra-booleana.shtml)

Porqué el álgebra de Boole

Obviamente, la respuesta es bastante sencilla. Todas las máquinas digitales funcionan con electricidad, a partir de diferencias de voltaje. Así que a cierto rango de voltaje le asignamos un cero y a otro le asignamos un uno (ceros y unos). De esta manera, gracias al álgebra de boole, podemos operar con estas diferencias de voltaje.
 

Tomado de:

Enamorado de la Ciencia

Como desarrollar el Pensamiento Algebraico en niños de Educación Primaria

El año 2010 llegó con sorpresas, la escuela tenía un nuevo direcotr, y el nuevo director lanzó un reto: enseñar álgebra desde el primer hasta el sexto grado de primaria. ¿Cómo? Ni el mismo lo sabía. Pero el reto estaba lanzado, tendriamos que empezar desde cero, repasar viejos libros empolvados (bueno, yo revise mis PDFs, incluido el Álgebra de Aurelio Baldor), crear secuencias didácticas para generar ideas algebraicas partiendo de la vida diaria de los cachorros, diseñar medios y materiales para cristalizar dichas secuencias y, finalmente, generar una propuesta curricular del álgebra en las escuelas primarias. ¡Todo un reto!

Y, ojo, no se trata de enseñar el álgebra a los niños tal como se enseña en la secundaria y en la mayor parte de los libros de texto. Cuando ser lanzó el reto se habló de generar pensamiento algebraico en los cachorros.

Y ¿Qué es el pensamiento algebraico? Lea:

El reto del Director de la escuela

Durante las dos últimas décadas del pasado siglo (años ochenta y noventa, cuando YO recién empezaba a luchar por ser el jefe de la manada) se estudiaba en las principales universidades del planeta la manera de facilitar el aprendizaje del álgebra a los cachorros de las escuelas (educación primaria). Inmediatamente se abrieron dos frentes: a) los que abogaban por introducir el álgebra desde los primeros grados de primaria con el fin de facilitar su aprendizaje en la secundaria y b) los que abogaban por generar un pensamiento algebraico en los cachorros, no necesariamente resilviendo ejercicios del tipo que nos encontramos en los libros de texto.

Es en este siglo XXI, globalizado y decadente, que las investigaciones sobre álgebra en la escuela primaria se han multiplicado, la gran mayoría de estos trabajos en inglés (Grrrrrrrrrr, qué coraje), y estas dos tendencias siguen en pugna.

Aquí en nuestra provincia (provincia de Barranca, región Lima Provincias) muchos colegios privados sigue el primer enfoque, es decir se introduce el álgebra desde los primeros grados pero, muchísimo ojo, se enseña el álgebra de la misma manera como se enseña en la escuela secundaria. Y, lo que es peor, se enseña el álgebra con el exclusivo fin de desarrollar problemas tipo y lograr que, en el futuro, los cachorros, ya jóvenes, puedan ingresar a un universidad.

Este enfoque, desgraciadamente, es el imperante en el Perú (mi gran país). ¿Por que digo desgraciadamente? Por dos razones:

a) En primer lugar por la gran distorsión (o aberración) que es señalar el fin de la educación básica (primaria y secundaria) como el ingreso a la Universidad.

¿Y dónde queda la felicidad? Grrrrrrrrrrrrrrrrrr!!!!! ¡Se supone que estudiamos para ser felices en el futuro! ¿Y dónde queda la libertad? Sólo se alcanza la felicidad cuando se es libre, libre como individuo y libre como colectivo (como sociedad). Y sólo se es libre cuando se es consciente, consciente del mundo social y natural en que estamos inmersos, consciente de nuestra historia, de nuestro potencial como sociedad y, sobre todo, consciente de las trabas que nos impiden ser felices y ser libres.

Pero la sociedad de consumo, tecnocrática, burocrática, injusta y deshumanizante en que vivimos nos responde: ¿Felicidad? ¿Libertad? Esas son estupideces (y no se por que se me viene a la mente la imagen de la hiena Cipriani). Y los líderes consumistas, tecnocráticos, burocráticos injustos y deshumanizados nos advierten: Y, menos, se dediquen a hablar sobre la educación como instrumento para la transformación y perfeccionamiento de la sociedad, por que sino te cierro el blog, la radio, el periódico o la editorial y encima te meto en una carceleta (y se me viene a la mente el jabalí García P.).

Pero gran número de padres de familia, sobre todo aquellos que aún no sabían leer cuando el jabalí García lo embarraba todo por vez primera, envían a sus hijos a los colegios privados (de 80 lucas al mes) para que sus hijos tengan ingreso directo a la universidad.

b) Y lo peor de todo, casi todos estos centros privados de deformación enseñan matemáticas y álgebra de manera libresca, teórica, memorística y, por ende, aburrida. Parten de conceptos, leyes, fórmulas. No enseñan a los niños la esencia de la matemática que es buscar y encontrar relaciones entre los objetos del mundo que nos rodea, ya sea en cantidades o en magnitudes. Y mucho menos buscan que los alumnos encuentren maneras de aplicar los conocimientos matemáticos en nuestra vida real y cotidiana: desde la resolución de problemas hasta la creación de modelos matemáticos.

Pero que se puede esperar de los promotores de estos centros de deformación que contratan a jóvenes universitarios en vez de docentes titulados y calificados, amén de otorgarles un mísero salario (y encima a destiempo y sin colocarlos en planillas). Y ni hablemos de los libros de texto Corefo, Coveñas, etc. (bueno, si hablaremos de ellos, pero será en otro post).

Las escuelas públicas contamos con un diseño curricular desfasado y chapucero, antihistórico e idealista; donde no se contemplan temas como el descubrimiennto de la ciudad de Caral, los ocho planetas del sistema solar, la vida y obra de Simón Bolívar o de Túpac Amaru II, la clonación de la oveja Dolly o cómo funcionan los celulares e Internet. Y, como ya podrán imaginarse, menos hablarán de pensamiento algebraico.

Por lo tanto el reto del director es tomado como:

a) un programa para revivir la investigación educativa y promover la innovación permanente en la forma de enseñar y

b) un medio para generar el pensamiento algebraico en los cachorros, enfoque que debe nacer de la vida diaria y debe culminar en la vida diaria también.



El proyecto Álgebra Fácil (del profesor Leoardo Sánchez Coello)

Con un rugido largo y potente asumí el reto y me puse manos a la obra sin pérdida de tiempo, busqué todos los libros que tenía sobre álgebra y, como podrán adivinar, no encntré nada sobre álgebra para niños. Entonces ingresé a la red y,¿qué creen?, tampoco encontré gran cosa, salvo investigaciones parciales,y casi todas ellas, en inglés (Grrrrrrrrr!!!!)

Entonces se abrío el cielo y cayó una luz sobre mi cabeza. Me iluminé y descubrí la VERDAD: Tengo que hacer todo este trabajo por mi mismo.

Les dejo a continuación la primera parte de mi quehacer que, en parte de fichas de trabajo, estoy realizando.

Primera Parte: 

Algebra Facil 1 by conocerciencia

Y esta es la Segunda Parte: 

Algebra Facil 2 by conocerciencia

 

Reitero que no se trata de enseñar álgebra, sino de enseñar pensamiento algebraico. Dedebemos de considerar que: 

a) El ágebra es considerada una rama dura de la matemática y buscamos acercar a los cachorros al estudio de las cantidades y magnitudes de la manera menos traumática posible. 

b) El pensamiento algebraico es poder expresar, en lenguaje matemático, los diversos objetos, situaciones o relaciones del mundo en que vivimos; pasando de situaciones concretas a situaciones abastractas y de situaciones con relaciones sencillas a situaciones con relaciones complejas (Grrrrrrrr!!!! ¿qué tal me quedó la definición? ¿eh?).

Bien, ahora surge la pregunta ¿cómo representar los objetos algebraicamente? Pongamos un ejemplo para comprender mejor.

En primer lugar necesitamos materiales que los niños pueden encontrar fácilemnte en su entorno: fósforos, chapitas, clips, alfileres, botones, cajitas, mondadientes, frejoles, pallares, maicitos, etc...


Los cachorros, por lo general espontáneamente, empiezan a a grupar estos elemntos de diversas maneras, buscando siempre un patrón u orden.



Luego se dirá a los alumnos que representen un objeto cualquiera con una letra. De esta manera si tenemos dos objetos diferentes (como clips y palitos) denominaremos a unos objeto con la letra a y a otros objetos con la letra b (así tendriamos que los clips = a, y los palitos = b).

Simbolizamos, y si es necesario graficamos, en el pizarrón.



Entonces se les dirá a los cachorros:

¿Cuánto será a + b?

Los niños responderán que la respuesta es un clip y luego un palito.

Luego preguntamos:

¿Y cuánto será 2a + 2b?

Los niños respoderán que dos clips y dos palitos.

Luego vendría la exploración con material concreto.



También puede explorar realizando el proceso inverso, es decir los niños realizarán patrones de manera espontánea y luego crearán una expresión algebraica para cada patrón realizado.

Estos son los trabajos de los cachorros del 3º "H" de la escuela Los Pelones de Barranca. La ecuación que se les presenta es, por decirlo de alguna manera, la instrucción o la orden a seguir. Los cachorros, partiendo de dichas instrucciones, construyen sus seriaciones con materiales concretos. Vean:








Los patrones con objetos concretos desarrolan el sentido de orden y espacio en los alumnos así como su sentido estético. Y, no olvidemos nuestro objetivo, los cachorros han traducido al lenguaje algebraico el orden de detrminados objetos de su entorno inmediato: han representado objetos algebraicamente.

Ahora intentemos realizar experiencias similares con fotografías de animales, personas que se encuentran en determinado orden; también podemos salir al patio y construir con nuestros cuerpos diversos patrones; las direcciones (simbolizadas con flechas) también son representaciones algebraicas; los bloque lógicos y las diversas ordenaciones que se pueden hacer con ello también se pueden representar algebraicamente.

Por ejemplo tenemos esta seriación de bloque lógicos:



Estos bloque se pueden agrupar de acuerdo a la forma o al color. Veamos:

a) Por la forma. Si consideramos que:

a = círculo

b = cuadrado

Entonces las seriación se podría representar algebraicamente como:

3a + 3b

b) Por el color. Hay tres colores diferentes. Entonces:

a = rojo

b = amarillo

c = azul

Entonces las seriación se podría representar algebraicamente como:

a + b + c

Esto es sólo un inicio. Sé que se debe enseñar el algebra desde un perspectiva un tanto informal, buscando formas lúdica, relacionada con el mundo que nos rodea y, sobre todo, tomando el algebra como un medio para desarrollar y estructurar el pensameinto de los cachorros, el algebra siempre como un medio y no como un fin. Pero eso es todo lo que sé.

Y aunque no tengo aún bien claro el norte es maravilloso experimentar, convertir las aulas en laboratorios donde los cachorros y YO (el jefe de la manada) construimos, aprendemos y nos divertimos. Porqué ¿de que nos serviría el álgebra si no somos libres y felices? ¿De qué nos serviría el álgebra si no tenemos conciencia clara de la sociedad en la que vivimos y de la necesidad urgente de su transformación.

En la nueva sociedad que nos espera emplearemos el álgebra para construir caminos y puentes, hospitales y colegios, casas para ancianos y para huérfanos, pero también emplearemos el álgebra para descubrir nuevas medicinas, salvar vidas luego de terremotos, controlar epidemias y comprender mejor los ecosistemas... Y el álgebra también nos servirá para que no nos engañen con el vuelto y para pasar el rato, resolviendo ejercicios, cuando estemos aburridos.

Hasta la próxima:

Leonardo Sánchez Coello
leonardo.sanchez.coello@gmail.com