La raíz cuadrada de dos: El terror de los Pitagóricos

El primer intento serio de “hacer ciencia”, o por lo menos algo que nosotros, dudosos habitantes del siglo XXI, podamos considerar como ciencia, ocurrió en Mileto, una próspera colonia griega del Asia Menor, donde vivió Tales (de Mileto, obviamente) en el siglo VI a.C., del que cuentan que, basado en viejos datos babilónicos, predijo el eclipse total del 28 de mayo de 585 a.C. Verdadero o no, a veces la fecha de ese eclipse se pone como punto de arranque de la ciencia occidental.

Tales de Mileto y su escuela introdujeron una innovación absoluta en el pensamiento griego: separar lo natural de lo sobrenatural y establecer que los fenómenos naturales deben explicarse mediante causas naturales. Es la escuela de la physis. La escuela de Mileto dejó planteado un problema difícil: ¿por qué se debe aceptar tal o cual explicación (desde ya, los milesios estaban muy lejos de la idea de experimento)? Y ¿cómo podemos basar una teoría en la observación, sabiendo lo poco fiables que son los sentidos, y la empiria en general?

Problemas que fueron enfrentados por la escuela eleática (por Parménides de Elea, 540-470 a.C.), que frente al testimonio dudoso de los sentidos, opone un Ser permanente, inmóvil, continuo, eterno y sin atributos, al que sólo se puede acceder por la vía de la razón, olvidando los fenómenos, puramente contingentes (como quiere demostrar Zenón de Elea, discípulo de Parménides con la célebre paradoja de Aquiles y la tortuga). Pero un Ser sin atributos no puede darnos demasiado; el camino de Parménides no produce ciencia sino metafísica: en realidad, la escuela eleática lleva a la incipiente ciencia griega a un callejón sin salida. ¿Cómo salir del atolladero?

Los filósofos griegos siguieron: algunos tomaron un camino radical, como los atomistas (Demócrito y Leucipo), que fracturaron el ser en pequeñas partículas indestructibles y eternas: los átomos, infinitos, “increados”, tienen distintas formas y que se mueven permanentemente en el vacío. Y hubo, si se quiere, otra solución: las matemáticas, en las que la razón no tiene que discutir ni ocuparse de fenómenos, sino de relaciones puras. Ese es el camino que suscribió una escuela muy importante que se desarrolló a partir del siglo V en el sur de Italia, la escuela pitagórica. Los pitagóricos establecieron que la fuente de la realidad son los números. A la pregunta ¿cuál es el origen de las cosas?, respondieron: los números.

Es posible que esta idea haya partido del estudio de la música: descubrieron que hay relaciones numéricas precisas entre los sonidos; y estas relaciones, para nada evidentes, pudieron impulsarlos a dar el paso audaz de generalizar y proclamar que todas las cosas consisten en números. 

Así, la escuela pitagórica opta por el pensar y resuelve el problema milesio. Y fueron tal vez un poco más lejos de lo aconsejable: identificaron a la Justicia con el número 4 por tratarse del primer número cuadrado; al matrimonio con el 5, que representaba la unión del macho (3) con la hembra (2). Además, creían que todo el cielo era una escala musical, analizaron muchas propiedades de los números, trabajaron sobre los poliedros regulares, las medias aritméticas, geométricas y armónicas, acústica y astronomía, que era algo así como geometría aplicada. Desde ellos viene esa ligazón entre aritmética, música, astronomía y geometría que constituirá el quadrivium medieval. Propusieron un sistema, integrado por un fuego central alrededor del cual giraban veinte cuerpos envueltos en niebla, y dieron numerosas demostraciones; la más famosa es, desde ya, el teorema de Pitágoras).

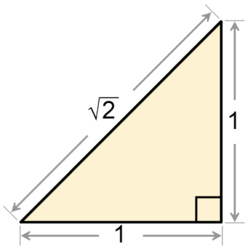
Pero he aquí que el teorema de Pitágoras llevó a una conclusión asombrosa, que puso en jaque todo el sistema pitagórico. Al fin y al cabo, si uno construye un cuadrado de lado 1, se puede ver fácilmente que, como el cuadrado de la diagonal es la suma de los cuadrados de los catetos, es 1 al cuadrado + 1 al cuadrado = 2. Y entonces la diagonal mide la raíz cuadrada de 2.

Resulta que los pitagóricos descubrieron también que la raíz cuadrada de 2 no es un número, que no hay ninguna fracción que la represente: la raíz de 2 es “a-logos”, es inexpresable: es irracional. Y sin embargo, la diagonal de un cuadrado de lado 1 está ahí, de manera neta y tan evidente; tiene una longitud real y extremos fijos, puede construirse una varilla de esa longitud concreta, pero esa longitud concreta no parece ser nada, no parece pertenecer a la esfera de lo posible... y sin embargo, está allí. Pero además, es imposible negar la existencia de la raíz cuadrada de 2, que no se produce en el terreno de la empiria, sino en el mundo puro de los números.

Ahora, ¡hay que imaginar el efecto que este descubrimiento tuvo que tener en algunos de los primeros pitagóricos! Ellos suponían que todo consiste en números y que el conocimiento expresa relaciones entre números (enteros o fraccionarios). Pero he aquí que una entidad, que ciertamente pertenece a la ciencia, la diagonal de un cuadrado, no puede ser expresada con números enteros, no puede existir. Es decir, tenemos algo concreto y ese segmento, que está ahí no es un número, no es nada. Y la medida de la diagonal de un cuadrado de lado 1 tampoco es nada. ¡Pero la diagonal de ese cuadrado está ahí! ¿Cómo puede ser que a un segmento no corresponda ninguna longitud?

Un ejemplo del terror que produjo ver que algo tan simple como la raíz cuadrada de 2 era un irracional es la leyenda según la cual un pitagórico, Hipaso, divulgó el secreto y pereció ahogado como castigo divino por su acción. Y es que la escuela pitagórica se había embarcado en un callejón sin salida. Construyeron todo un edificio científico, místico, que les parecía muy sólido, y de repente aparece este asunto que amenaza con precipitar toda la escuela en el abismo. Los pitagóricos se enfrentan a este dilema y no lo pueden resolver. Han fracasado en su teoría de que todo está constituido por números, aunque la influencia que ejercieron siguió resonando a través de los siglos, y la encontramos aún en Kepler.

Y es que el problema con que se enfrentaron no es fácil de resolver, la raíz de 2, como descubrieron los pitagóricos, desde ya no es una fracción: no hay número entero ni fraccionario alguno que multiplicado por sí mismo nos reproduzca exactamente al 2. Actualmente escribimos raíz cuadrada de 2 como 1,14142135624 y agregamos una serie de puntos suspensivos que significan que la fracción decimal no tiene fin, que el número de decimales (no periódicos) es infinito. Es lo que ahora llamamos (quizás en homenaje a Pitágoras) un número irracional.

El terror de los pitagóricos ante la raíz de 2 es fácil de entender, porque nosotros, hoy, en el fondo, seguimos siendo pitagóricos. No creemos, como Pitágoras, que todo es número, pero sí que las matemáticas subyacen al mundo empírico; que de un modo misterioso organizan la empiria, que aquello que es matemáticamente posible es y que aquello que no es matemáticamente posible, no es.

Tomado de:

Página 12 

Bonus:

La biografía de Pitágoras, y detalles curiosos de los pitagóricos, en esta presentación:

Conocer Ciencia - Pitágoras y el número from Leonardo Sanchez Coello

La demostración más elemental de la irracionalidad de raíz de dos

A estas alturas de la película creo que es bastante conocido que el número raíz de dos, , es un número irracional. Es decir, que no puede expresarse como una fracción con numerador y denominador números enteros.

Hay muchas formas de demostrarlo. De hecho aquí en Gaussianos hemos visto ya varias: la típica que usa reducción al absurdo (junto con una que usa descenso infinito) y una demostración geométrica muy interesante. Hoy vamos a ver la, posiblemente, demostración de la irracionalidad de raíz de dos más elemental que he visto nunca.

Comencemos con ella. Está bastante claro que las únicas posibilidades que pueden darse en una fracción son las siguientes: impar/impar, impar/par, par/impar y par/par.

La opción par/par se puede reducir a alguna de las otras tres, por lo que no es necesario considerarla.

Dicho esto, veamos que ninguna de las tres opciones puede dar como resultado . O lo que es lo mismo, que el cuadrado de cada una de ellas no puede valer 2. O lo que es igual, que al elevar al cuadrado cada una de ellas el numerador no puede ser el doble que el denominador. Hasta ahora bien, ¿verdad? Bien, pues vamos caso por caso:

• impar/impar Si elevamos un número impar al cuadrado obtenemos un número impar, por lo que al elevar esta fracción al cuadrado obtenemos otra fracción tipo impar/impar, y está bastante claro que un número impar no puede ser el doble que otro número impar, por lo que no puede ser igual a una fracción de este tipo.
• impar/par Si elevamos un número par al cuadrado obtenemos también un número par, por lo que aquí al elevar al cuadrado obtendremos una fracción del tipo impar/par. Pero un número impar no puede ser el doble de un número par, por lo que tampoco puede ser igual a una fracción de este tipo.
• par/impar Por lo visto anteriormente, el cuadrado de esta fracción daría también una del tipo par/impar, y aquí en principio sí que podría ser que el numerador fuera el doble del denominador. Pero en realidad no es así, ya que un número par al cuadrado da un múltiplo de 4, y es claro que un múltiplo de 4 no puede ser el doble de un número impar (porque en realidad es el doble de un número par). Por tanto tampoco puede ser igual a una fracción así.

Lo que hemos obtenido es que no puede ser igual a ninguno de los tipos de fracciones posibles donde el numerador y el denominador son números enteros. En consecuencia, no es un número racional, hecho que unido a que sí es un número real nos lleva a que es un número irracional

Sencilla, ¿verdad? ¿Conocéis alguna otra demostración más elemental que ésta?

Fuente:

Gaussianos