Stephen Jay Gould, el mejor paleontólogo del siglo XX

¿Por qué ningún animal se desplaza sobre ruedas? ¿Las cebras son blancas con franjas negras, o negras con franjas blancas? Con preguntas como estas, el paleontólogo, biólogo evolutivo y divulgador científico Stephen Jay Gould (10 de septiembre de 1941-20 de mayo de 2002) provocaba a sus colegas y a sus lectores, para luego explicar algunas de las ideas más complejas de la evolución. Así como Charles Darwin, Gould se dedicó a entender todos los aspectos de la naturaleza y desveló enigmas que atormentaban a sus compañeros desde que el maestro inglés publicara “El origen de las especies”, en 1859. Él completó las teorías de Darwin con nuevas hipótesis e inició tres debates científicos que llevaron a sus colegas a repensar las ideas del padre de la evolución y que le convirtirían en el mejor paleontólogo del siglo XX.

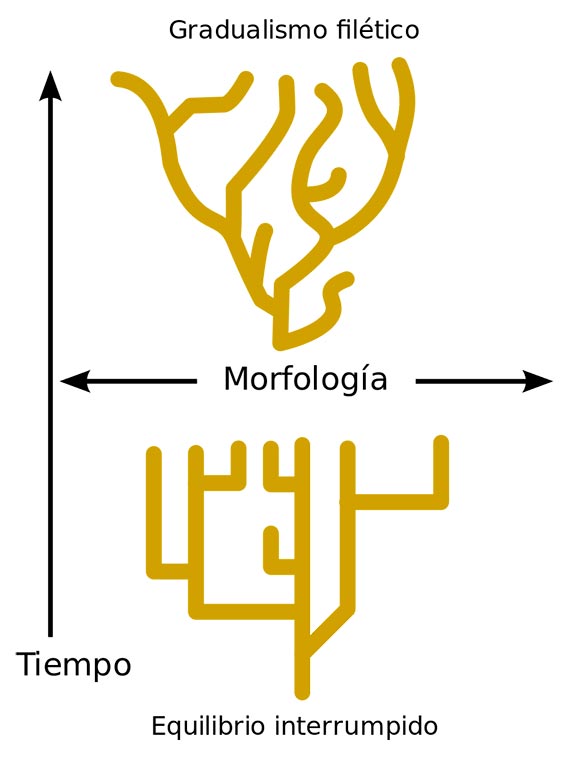
En la década de 1970, durante su doctorado en la Universidad de Columbia, Gould y Niles Eldredge analizaban fósiles para entender cómo operaba la evolución, hasta que ambos dieron con un problema aparentemente irresoluble. No encontraban cambios graduales en las especies, como preveía Darwin. Según su teoría los organismos de una misma especie compiten entre sí y el mejor adaptado al ambiente sobrevive y pasa a sus descendientes sus características; y así, de manera lenta y gradual, se van produciendo cambios en las generaciones futuras. Gould y Eldredge encontraron largos períodos de casi total estabilidad, sin cambio alguno, eventualmente interrumpidos por brotes de nuevas especies que aparecían de repente.

Darwin ya se había enfrentado al mismo problema más de un siglo antes, pero argumentó que la falta de fósiles se debía a la dificultad de encontrarlos. Gould y Eldredge llegaron a otra conclusión y publicaron en 1972 la teoría del equilibrio puntuado, según la cual las especies dan saltos evolutivos y cambian profundamente de un momento a otro, después de permanecer estables por mucho tiempo. Gracias a la controvertida tesis, Gould se ganó las críticas de grandes científicos como los biólogos evolutivos John Maynard Smith y Richard Dawkins.

Lea el artículo completo en: El País (España) 

El sistema para aprender cualquier cosa (también alemán) en cuatro semanas

Idiomas, cocina, guitarra... ¿qué quiere saber?

Entre el trabajo, las horas que pasamos en el transporte, el cuidado de los hijos, las tareas domésticas... ¿Cuánto tiempo le queda al día para aprender cosas nuevas? ¿Hace cuántos años que se propuso aprender a tocar la guitarra, a chapurrear alemán, a hacer esferificaciones en la cocina o a bailar claqué?

Tenemos una buena noticia: solo necesita 20 horas en total para ser razonablemente hábil en cualquiera de esos campos. Y si no sabe de dónde sacar esa cantidad de tiempo, Benjamin Franklin nos dejó en herencia el secreto para encajar las sesiones que necesita en una agenda apretada como la suya.

La curva de aprendizaje se hace más plana a partir de las primeras 20 horas

Lo primero que debe aceptar es que probablemente no vaya a convertirse en un experto: no va a dar conciertos de guitarra en el Teatro Real ni a emplearse como intérprete de chino, pero sí adquirirá los conocimientos necesarios para defenderse. En 20 horas podrá situarse en un punto suficientemente alto de la curva de aprendizaje, el diagrama que ya en 1885 definió el filósofo y psicólogo alemán Hermann Ebbinghaus y que hoy se utiliza, entre otras cosas, para evaluar procesos de productividad y de calidad en el ámbito empresarial. Consiste en el cruce de dos variables: el nivel de conocimiento de una materia y el tiempo que se dedica a su aprendizaje.

Según explica el escritor y conferenciante Josh Kauffman en su bestseller The first 20 hours. How to learn anything fast (Las primeras 20 horas. Cómo aprender cualquier cosa rápidamente), como se puede ver en la curva —junto a estas líneas—, hay un periodo inicial en el que se adquiere la mayoría de los conocimientos de una materia. A partir de ahí, el tiempo que se dedique a esta actividad será de perfeccionamiento, pero la mejoría será apenas imperceptible. Para Kauffman ese tiempo de escalada no son más de 20 horas.
Pero, ¿de dónde sacarlas y cómo distribuirlas? El político, periodista e inventor Benjamin Franklin usaba un método que también aplican muchas de las personas con éxito, según el análisis que ha hecho Michael Simmons, autor de bestsellers como The Student Success Manifesto (el manifiesto del éxito estudiantil) y escritor para cabeceras como Forbes, Fortune y Time. Simmons ha encontrado un patrón que se repite y al que ha llamado "la regla de las cinco horas". Franklin, asegura, solía arreglárselas para dedicar al menos una hora al día de lunes a viernes a aprender algo.

El artículo completo en: El País (España)

El método Singapur para razonar problemas verbales elementales

Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con

Un ejemplo

Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?

Solución algebraica
Sea x la cantidad recibida de su madre. Entonces, el problema se modela de la siguiente manera: 7+x=2(2+x). Es decir, x=3 --recibieron 3 pesos de su madre.

Elemental ¿no es cierto? Pues sí pero no para un niño de quinto año (11 años). Y ello porque no hay álgebra en aula de primaria. (No se le puede enseñar porque aún no alcanza la etapa de pensamiento formal en su desarrollo cognitivo --según se sabe.)

En la escuela primaria se prepara a los alumnos en aritmética, y se esperaría que la forma de enseñarla los prepare para el álgebra, la cual tiene que esperar la educación secundaria.

Y, sin embargo, el problema está al alcance de un niño de 11 años (bueno, por lo menos en teoría). Por ejemplo, lo puede resolver por tanteos: se propone al cantidad recibida y se verifica si cumple la condición del "doble que". Pero ese método tampoco es enseñado, pues se cree que es un método natural de resolverlo.

Otra forma de resolverlo es diagramático --el cual sí se enseña en Singapur. Sería más o menos como sigue:

Los datos del enunciado se representan gráficamente (la representación gráfica ayuda al razonamiento).

Se agrega al diagrama la cantidad recibida --la cual no se sabe cuánto es pero... Una vez teniendo el diagrama ya se puede razonar sobre él. Y se puede usar el método del "número escondido": la cantidad recibida más 2 es 5, por tanto la cantidad recibida es 3.

Entre lo concreto y lo abstracto está el diagrama

Todo mundo está de acuerdo en que, en el desarrollo cognitivo de los niños, primero es lo concreto y después lo abstracto. Pero intermedio entre esas dos formas de razonar está el razonamiento diagramático. Y el método Singapur de resolución de problemas razonados le apostó a esa hipótesis (clásica pero poco apreciada). El lema del currículum de la educación matemática básica en Singapur refleja esa apuesta: concreto, pictórico, abstracto.

Nota geográfica y económica: Singapur es un pequeño país en el extremo sur de la península de Malasia, sin ser parte de ésta pues es una isla --de hecho son varias islas. Añadiré que, de acuerdo a su economía, es uno de los "cuatro tigres asiáticos" --siendo los otros tres Korea del Sur, Hong Kong y Taiwan.

Ilustración del razonamiento diagramático

Ya en otra ocasión había escrito un post sobre razonamiento diagramático y el método Singapur

En esta ocasión voy continuar ese post, ilustrando el método diagramático de Singapur con algunos problemas razonados. Voy a resolver el más difícil y los restantes se quedan como un ejercicio para el lector.

Problema 1 (edades desfasadas): Beto tiene el doble de la edad que Sandra tenía cuando Beto tenía la edad que ahora tiene Sandra. Cuando Sandra tenga la edad que ahora tiene Beto, la suma de sus edades será 45 años. Calcular la edad de Sandra.

Solución diagramática


(Hay que saber que la diferencia de edades se mantiene constante en el tiempo.) Sea d la diferencia de edades y representemos con b la edad de Beto y con s la edad de Sandra.

Desplazando las edades de Sandra y Beto d años hacia el pasado, se hace evidente que Beto tiene 4d años.

Desplazando las edades d unidades hacia el futuro, se puede ver que 5d+4d=45. Es decir, d=5. Por tanto, Beto tiene 20 y Sandra 15.

Problema 2 (suma y diferencia): Las edades de Beto y Sandra suman 35 años, y su diferencia es 5. Calcularlas.

Problema 3 (la mula y el burro): Le dice el burro a la mula "si me ayudaras con 10 ladrillos llevaríamos la misma carga". Y la mula le contesta "si tú me ayudaras con 10 llevarías el doble que yo." Calcular los ladrillos que lleva cada uno.

Problema 4 (Padre e hijo): El padre es 45 años mayor que su hijo. En 6 años éste tendrá la cuarta parte de la edad de su padre.

Problema 5. Dos números suman 60, y el mayor es cuatro veces el menor.

Problema 6. Alex tiene 48 pesos más que Arturo y éste la séptima parte de loque Alex tiene. 

Se invita al lector a intentar resolver los problemas en el post Razonados de álgebra sin álgebra utilizando el método Singapur.

Tomado de:

Mate Tam

Teorema de la altura: una prueba visual

En nuestra sociedad globalizada, en la que el espectáculo y la diversión han sido puestos en el centro por los mass media, es muy difícil ser profesor, de cualquier cosa, pero sobre todo de matemáticas. ¿Tiene que ser convertida el aula  en un reality show para atraer la atención de nuestros estudiantes?

Con demasiada frecuencia sigo escuchando el argumento de que las matemáticas son difíciles porque el profesor no sabe enseñarlas. Y el argumento se refuerza con anécdotas de la vida escolar adolescente. Puedo leer entre líneas --es decir, puedo "maliciar" en ese argumento-- la hipótesis oculta de que el profesor no sabe armar un espectáculo con su tema a enseñar. Mínimo, que hay una forma correcta (la cual puede depender del opinante) de enseñar las matemáticas mientras todas las demás están equivocadas. Permítaseme documentar la idea con un relato.

¿Por qué nadie me lo había explicado así?

Recientemente un profesor (de sociología) me comentaba muy entusiasmado que "ahora sí había entendido el binomio al cuadrado". Según le entendí, había asistido a una conferencia sobre educación matemática y el expositor había planteado el binomio al cuadrado de manera diagramática (o visual). Según su explicación, la visualidad que tanto impactó a mi amigo habría sido ésta:

Yo le comenté que esa manera de ilustrar el binomio al cuadrado está desde hace ya tiempo en los libros de secundaria y que no entendía qué era lo extraordinario de ello. El sociólogo replicó que si así le hubieran enseñado a él, posiblemente habría elegido estudiar la licenciatura en matemáticas, bla, bla , bla. La conversación continuó un poco más, pero ante el entusiasmo de mi sociólogo desistí de indagar el motivo de su entusiasmo.

Pues es muy difícil bajar a un estusiasta de su nube. Lo que pude inferir de su conversación es que, por alguna razón, se conectó al tema de la conferencia como nunca antes lo había hecho y tuvo una revelación... Aparte está el hecho de que el binomio al cuadrado requiere un mínimo de conocimientos previos para su comprensión --en contraste con otros productos notables como la factorización por las fórmulas de Vieta.

Por otro lado, las pruebas visuales están orientadas a atraer la atención del aprendiz --lo cual está cañón, pues una prueba visual es incomparablemente menos atractiva que el espectáculo montado por un videojuego. Además de que su utilidad didáctica de largo plazo es cuestionable --pues, en el caso de los productos notables, lo que verdaderamente estaría en juego ahí es la regla distributiva... Quiero decir, la prueba visual es atractiva y cumple una función didáctica pero...

Teorema de la altura y su contexto

Un poco como el profesor de sociología del relato --y a pesar de las contraindicaciones de las pruebas visuales-- voy a compartir con los lectores de MaTeTaM una prueba visual del teorema de la altura que logró entusiasmarme (aunque quizá por razones diferentes a las de mi sociólogo). Tiene la desventaja de que no es para todo público (como la del binomio al cuadrado). Pues hay que saber dos o tres cosas de semejanza de triángulos rectángulos.

La configuración geométrica para el teorema de la altura es un triángulo ABC, rectángulo en A, con h la altura relativa a la hipotenusa y p y q los segmentos en que aquélla divide a ésta. En otras palabras, si llamamos D al pie de la altura, entonces h=AD,p=BD,q=DC

Es fácil ver --por complementariedad-- que los triángulos CDA y ADB son semejantes. De aquí que sus lados sean proporcionales. Es decir 

BDDA=ADDC

O bien, sustituyendo las longitudes de los segmentos,

ph=hq

Este teorema se acostumbra formular como

h2=pq

Y se enuncia así:

En un triángulo rectángulo, la altura asociada a la hipotenusa es media geométrica de los segmentos en que la hipotenusa queda dividida por la altura.

Importancia didáctica del teorema de la altura

A pesar de que es elemental y su demostración es consecuencia directa de una evidente semejanza de triángulos, este teorema es importante porque permite al aprendiz ejercitar su comprensión de la semejanza de triángulos. Y aprovechando su cercanía con el teorema del cateto, se puede armar una secuencia didáctica que culmine en la demostración clásica más elemental del teorema de Pitágoras. Enseguida las demostraciones del teorema del cateto y el de Pitágoras.

Según la notación usual, el cateto opuesto al vértice B se denota con b y el opuesto al vértice C con c. Entonces, con referencia a la figura anterior, el teorema del cateto diría: b2=qa,c2=pa. Sumando ambas ecuaciones se obtiene Pitágoras.

La prueba visual

Con referencia de nuevo a la figura anterior, imaginemos que recortamos el triángulo ABC sobre su altura AD y que separamos los triángulos CDA y ADB --los cuales son semejantes, como se dijo arriba. Entonces, si giramos el triángulo ADB 90 grados sobre A, obtenemos una configuración como la siguiente.

Y si intercambiamos las posiciones de los dos triángulos se obtiene la siguiente configuración:

 

Y si tomamos una copia del triángulo CDA, ambas configuraciones se combinan en la siguiente:

La prueba visual consiste en observar que los triángulos BCS y A′AT son rectángulos y congruentes y, en consecuencia, tienen la misma área. Así que si a cada uno de ellos le quitamos los dos triángulos cortados del original, las áreas que quedan son iguales. Es decir, h2=pq.

Tomado de:

MateTam

Diagramas Causa-Efecto

DIAGRAMAS CAUSA-EFECTO

La efectividad de las estrategias de Aprendizaje Visual para la construcción y comprensión de nuevos conocimientos y para desarrollar habilidades de pensamiento de orden superior, es reconocida por docentes del mundo entero. 

La elaboración de diagramas visuales ayuda a los estudiantes a procesar, organizar y priorizar nueva información, de manera que puedan integrarla significativamente a su base de conocimientos previos. Además, les permite identificar ideas erróneas y visualizar patrones e interrelaciones en la información, factores necesarios para la comprensión e interiorización profunda de los conceptos. 

Sin embargo, para que la aplicación en el aula de las diferentes estrategias de Aprendizaje Visual sea realmente efectiva, es necesario tener en cuenta los objetivos de aprendizaje que se desea que los estudiantes alcancen. 

Por ejemplo, si lo que se quiere es que los estudiantes ubiquen, dentro de un periodo de tiempo determinado, los sucesos relacionados con el descubrimiento de América para que visualicen y comprendan la relación temporal entre estos, el método u organizador gráfico idóneo es una Línea de Tiempo. Por el contrario, si lo que se desea es que los estudiantes comprendan la relación entre los conceptos mas importantes relacionados con el descubrimiento de América tales como: Nuevo mundo, conquista, colonia, economía y navegación, la herramienta idónea es un Mapa Conceptual. 

Así mismo, cuando el objetivo de aprendizaje es que los estudiantes descubran las causas de un problema o de un suceso, o las relaciones causales entre dos o más fenómenos, el organizador gráfico ideal es un Diagrama Causa-Efecto. 

Siguiendo con el ejemplo anterior, al elaborar este diagrama los estudiantes identificarían cómo el cambio de las concepciones sobre la forma de La Tierra (redonda), el bloqueo del comercio de especias por el Mediterráneo [1], la posición estratégica de España en la Península Ibérica y los avances tecnológicos en materia de navegación, fueron eventos que, relacionados unos con otros, causaron el descubrimiento de América.

Los Diagramas Causa-Efecto ayudan a los estudiantes a pensar sobre todas las causas reales y potenciales de un suceso o problema, y no solamente en las más obvias o simples. Además,son idóneos para motivar el análisis y la discusión grupal, de manera que cada equipo de trabajo pueda ampliar su comprensión del problema, visualizar las razones, motivos o factores principales y secundarios, identificar posibles soluciones, tomar decisiones y, organizar planes de acción. 

El Diagrama Causa-Efecto es llamado usualmente Diagrama de “Ishikawa” porque fue creado por Kaoru Ishikawa, experto en dirección de empresas interesado en mejorar el control de la calidad; también es llamado “Diagrama Espina de Pescado” por que su forma es similar al esqueleto de un pez: Está compuesto por un recuadro (cabeza), una línea principal (columna vertebral), y 4 o más líneas que apuntan a la línea principal formando un ángulo aproximado de 70º (espinas principales). Estas últimas poseen a su vez dos o tres líneas inclinadas (espinas), y así sucesivamente (espinas menores), según sea necesario.

 

Esquema elaborado con el software CmapTools (http://www.eduteka.org/HerramientasVisuales.php)

Aunque la mayoría de Diagramas Causa-Efecto se representan de esta manera, estos se pueden elaborar siguiendo otros formatos. En la dirección http://www.educationoasis.com/curriculum/GO/cause_effect.htm usted puede encontrar otros modelos para construir Diagramas Causa-Efecto.

 

PASOS PARA CONSTRUIR UN DIAGRAMA CAUSA-EFECTO

1. IDENTIFICAR EL PROBLEMA

Identifique y defina con exactitud el problema, fenómeno, evento o situación que se quiere analizar. Éste debe plantearse de manera específica y concreta para que el análisis de las causas se oriente correctamente y se eviten confusiones. 

Los Diagramas Causa-Efecto permiten analizar problemas o fenómenos propios de diversas áreas del conocimiento. Algunos ejemplos podrían ser: la falta participación de los alumnos del grado 9-A en las votaciones estudiantiles, la extinción de los dinosaurios, el establecimiento del Frente Nacional en Colombia, la migración de las aves, entre otros. 

Una vez el problema se delimite correctamente, debe escribirse con una frase corta y sencilla, en el recuadro principal o cabeza del pescado, tal como se muestra en el siguiente ejemplo: Bajo rendimiento en Matemáticas.

Diagrama elaborado con el software SmartDraw (http://www.eduteka.org/HerramientasVisuales.php)

El artículo completo en:

EDUTEKA

Diagrama de Tallos y Hojas

El diagrama "tallo y hojas" (Stem-and-Leaf Diagram) permite obtener simultáneamente una distribución de frecuencias de la variable y su representación gráfica. Para construirlo basta separar en cada dato el último dígito de la derecha (que constituye la hoja) del bloque de cifras restantes (que formará el tallo). 

Esta representación de los datos es semejante a la de un histograma pero además de ser fáciles de elaborar, presentan más información que estos.
Ejemplos

• Horarios de trenes
• Edad de 20 personas
• Comparar dos distribuciones

Horarios de trenes

Basándome en un articulo de Juan C. Dürsteler en InfoVis.net, tomamos como ejemplo un horario de trenes confeccionado a partir de un díptico de la línea Castelldefels-Barcelona/Sants recogido en la estación de Renfe. Originalmente el horario ocupa una tabla de 10 filas y 9 columnas más una columna "viuda" con el tren de las 22:38. Un total de 91 campos con formato hh.mm cada uno, 455 caracteres.
Díptico original Trayecto Castelldefels -> Barcelona-Sants  

     5.03  7.32   9.02  11.07  13.32  15.07  16.50  18.32  20.07  22.38
     6.02  7.37   9.07  11.32  13.37  15.20  17.02  18.37  20.20
     6.18  7.50   9.24  11.37  13.50  15.32  17.07  18.50  20.32
     6.37  8.02   9.32  12.02  14.02  15.37  17.20  19.02  20.37
     6.48  8.05   9.37  12.07  14.07  15.50  17.32  19.07  20.50
     6.55  8.20  10.02  12.32  14.20  16.02  17.37  19.20  21.02
     7.02  8.24  10.07  12.37  14.32  16.07  17.50  19.32  21.07
     7.07  8.32  10.32  13.02  14.37  16.20  18.02  19.37  21.20
     7.20  8.37  10.37  13.07  14.50  16.32  18.07  19.50  21.32
     7.25  8.51  11.02  13.20  15.02  16.37  18.20  20.02  21.37

En el diagrama Stem & Leaf se representa la hora a la izquierda de la barra de separación | y los minutos de la salida de cada tren a la derecha. La frecuencia de los trenes se deduce fácilmente de la longitud de las filas y es, además, muy fácil ver en que minutos de cada hora pasan típicamente los mismos.

Castelldefels -> Barcelona-Sants Diagrama Stem & Leaf 

05 | 03
06 | 02 18 37 48 55
07 | 02 07 20 25 32 37 50
08 | 02 05 20 24 32 37 51
09 | 02 07 24 32 37    
10 | 02 07 32 37     
11 | 02 07 32 37     
12 | 02 07 32 37     
13 | 02 07 20 32 37 50       
14 | 02 07 20 32 37 50    
15 | 02 07 20 32 37 50
16 | 02 07 20 32 37 50
17 | 02 07 20 32 37 50
18 | 02 07 20 32 37 50
19 | 02 07 20 32 37 50
20 | 02 07 20 32 37 50
21 | 02 07 20 32 37
22 | 38

Por otra parte, dado que a algunas horas se repite exactamente el horario de los trenes se puede reducir aún más el tamaño del gráfico, sin perder información  y ganando en claridad.

Castelldefels -> Barcelona-Sants Diagrama Stem & Leaf reducido

                                   05 | 03
                                   06 | 02 18 37 48 55
                                   07 | 02 07 20 25 32 37 50
                                   08 | 02 05 20 24 32 37 51
                                   09 | 02 07 24 32 37
                             10 11 12 | 02 07 32 37
              13 14 15 16 17 18 19 20 | 02 07 20 32 37 50
                                   21 | 02 07 20 32 37
                                   22 | 38

Al final tenemos 59 campos de 2 dígitos, 118 caracteres más los separadores, es decir 4 veces menos dígitos que con el horario original, menos espacio y más claridad.

Esto nos da idea de que una disposición apropiada de los datos puede ser doblemente informativa y que la representación gráfica puede contribuir enormemente a la percepción de patrones y a la comprensión de la naturaleza de los fenómenos.

Edad de 20 personas

Supongamos la siguiente distribución de frecuencias 

   36  25  37  24  39  20  36  45  31  31

   39  24  29  23  41  40  33  24  34  40

que representan la edad de un colectivo de N = 20 personas y que vamos a representar mediante un diagrama de Tallos y Hojas. 

Comenzamos seleccionando los tallos que en nuestro caso son las cifras de decenas, es decir 3, 2, 4, que reordenadas son 2, 3 y 4. 

A continuación efectuamos un recuento y vamos «añadiendo» cada hoja a su tallo
 

Por último reordenamos las hojas y hemos terminado el diagrama 

Comparar dos distribuciones

Podemos comparar, mediante estos diagramas, dos distribuciones. Supongamos una segunda distribución 

   35  38  32  28  30  29  27  19  48  40

   39  24  24  34  26  41  29  48  28  22

De ella podemos elaborar sus diagrama de Tallos y Hojas y compararla con la anterior. 

 

Fuentes:

Estadística para todos

Universidad Nacional de Colombia

Razonamiento diagramático en problemas de factorización

En este post voy a comentar sobre el método de reagrupamiento para factorizar una ecuación cuadrática y su correspondiente solución diagramática. Ilustro con un caso particular de toda

Una familia de problemas cuadráticos

En una ecuación cuadrática, si se puede factorizar entonces se puede representar como rectángulo --con uno de sus factores la base y el otro la altura.

Consideremos el problema de factorizar la ecuación cuadrática

ax2+(a+b)x+b=0

(donde a,b son enteros positivos).
Este problema es, en realidad, toda una familia de problemas, uno para cada par de números enteros positivos a,b. Por ejemplo, si a=2011,b=1, se tiene el problema 1A del concurso estatal OMM Tamaulipas 2012 

Por esa razón, puede ser de alguna utilidad como generador de problemas cuadráticos para los profesores de matemáticas de bachillerato. Discutamos ahora su

Solución

El método de reagrupamiento nos lleva a la siguiente ecuación equivalente:

ax2+ax+bx+b=0

Y se logra ver que es posible factorizar la ecuación como

ax(x+1)+b(x+1)=(ax+b)(x+1)=0

Y esa factorización se puede representar como un rectángulo de base x+b y altura x+1
(Nota: por el teorema del residuo, es también relativamente fácil darse cuenta que x=−1 satisface la ecuación --y lo que sigue es dividir entre x+1 para obtener el otro factor.)

Discusión

La pregunta ahora es ¿es posible factorizar una cuadrática de manera diagramática? Y, bueno, uno podría decir: sí, si es de la forma antes mencionada.

Y ¿cómo se reconoce una ecuación de la forma antes mencionada? Bueno, debería ser claro que el truco es que todos sus coeficientes sean positivos y que la diferencia entre el coeficiente de la x y el de la x2 sea igual al término independiente.

Consideremos el caso de la ecuación 5x2+7x+2. Es claro que esta ecuación satisface los dos requisitos mencionados. Y, bueno, uno entonces podría explicar a sus estudiantes:

Vean que si tomamos este rectángulo de base 5x y altura x su área es 5x2. Pero como 7x=5x+2x entonces agregando este otro rectángulo de base 5x y altura 1, y este otro --a la derecha-- de base 2 y altura x, ya tenemos el segundo término representado en estos rectángulos. Y como este otro rectángulo de la esquina arriba a la derecha es de base 2 y altura 1, entonces ya tenemos el término independiente. ¿OK? Y ahora ¿cuáles son las dimensiones de este rectángulo que hemos formado con los términos de la ecuación cuadrática? Piénsenlo un rato y me lo dicen. Etcétera, etcétera.

Esta exposición didáctica de la factorización de este tipo de ecuaciones cuadráticas es efectista. De hecho no aporta nada que no esté ya en el método de reagrupamiento.

Pero tiene la ventaja --posiblemente-- de dejar al aprendiz intrigado, y posiblemente asombrado... (se preguntará acaso sobre la forma en que los términos se acomodaron tan perfectamente en un rectángulo). Y si llega a descubrir el truco entonces la exposición fue un éxito. (Claramente, para el indiferente cualquier tipo de exposición es igualmente aburrida...)

Los saluda
jmd

Tomado de:

Mate Tam