Hacer una o muchas colas en el supermercado: ¿qué nos dice la estadística?

Acostumbrado a las colas "tradicionales" en los supermercados, donde cada caja tiene su propia cola, hace años me sorprendió ver que algunas cadenas usaban un método novedoso: la cola única para todas las cajas. Fue en UK, y hasta hace poco no han empezado a adoptar ese modelo algunas grandes superficies españolas.
A primera vista no es trivial decir qué sistema es mejor. En el post de hoy haremos un análisis estadístico (incluyendo simulaciones) con el que dejaremos bien claro que el sistema de única cola es mucho mejor desde el punto de vista del cliente.

Los dos competidores: (izquierda) las colas tradicionales, (derecha) la cola única (Créditos imagen)

Los que hayan estudiado teleco ya sabrán que el modelado de este tipo de problemas forma un campo de las matemáticas en sí mismo: la Teoría de Colas. Piensa que además de en la cola del super, nos encontramos problemas muy parecidos en redes de telecomunicaciones (e.g. paquetes de datos esperando entrar o salir por un router), en programas informáticos (e.g. peticiones a un servidor), etc. por lo que hay mucha gente que lleva décadas estudiando todo esto a fondo. De hecho podemos remontarnos a hace un siglo, cuando Erlang calculó cuándo se saturarían las líneas telefónicas de una ciudad. En su honor se definió la unidad de carga en redes de telefonía.

Básicamente lo que nos interesa en el caso del supermercado es un único estadístico que mide directamente el nivel de cabreo del cliente: cuánto tiempo tiene que esperar antes de que le atiendan. Las dos alternativas de sistema son:

1. Una única cola y un número M de cajas para atender a clientes (1 cola / M cajas).
2. M cajas, cada una con su cola (M colas / M cajas).

En este tipo de estudios estadísticos no tenemos ni idea de cuándo llegarán los clientes, pero la sincronización es importante porque si llegan muchos a la vez se formarán colas más largas. Para modelar esto matemáticamente se asume que existe una distribución de probabilidad uniforme y constante de que aparezca un cliente, lo que lleva a una distribución exponencial de los períodos desde que llega un cliente hasta el siguiente.

Aunque parezca un modelo un poco rebuscado y artificial, es el mejor posible cuando se asume que cada persona va a su bola y llega a una hora que es independiente (estadísticamente) de lo que hacen los demás.

Distribución exponencial para distintos valores del parámetro (lambda), relacionado con el número medio de llegadas por unidad de tiempo.

Asumiremos que los clientes llegan a un ritmo de [Math Processing Error] por minuto, y que las cajas son capaces de atenderlos a un ritmo de [Math Processing Error] cada una. Así, el modelo de M cajas queda:

Para hacer una comparación justa, en el modelo de cola única asumiremos que llegan el mismo número de clientes por minuto, y por tanto entrarán en la cola con frecuencia de  [Math Processing Error] por minuto:

Desde el punto de vista del número de clientes atendidos por minuto, los dos sistemas son equivalentes. Es más, el tiempo medio que transcurre desde que un cliente llega hasta que se le atiende también son iguales, dividiendo el tiempo total de funcionamiento entre el número total de clientes que pasan por el sistema.

Pero desde el punto de vista del cliente, es mejor el sistema de cola única debido al sesgo de muestreo: si por lo que sea se forma un pequeño retraso en una de las M colas, ese retraso será "notado" por muchos clientes al haberse formado más cola. Que en ese mismo momento haya otros pocos clientes que encuentren cajas libres no es suficiente para bajar la media del tiempo de espera subjetivo.

Se pueden sacar fórmulas teóricas que dan la distribución de tiempos de espera para cada caso, pero hoy me apetecía más hacerlo experimentalmente, así que he programado un simulador de eventos discretos para estimar cuánto afecta la elección del sistema de cajas (si alguien deriva las fórmulas, ¡le agradecería que las dejase en los comentarios!).

La siguiente gráfica resume muy bien el resultado: son los tiempos medios que los clientes esperan hasta ser atendidos en cada uno de los sistemas (negro: cola única), para distintos valores de número de cajas abiertas (M=2, 5, 10 y 20).

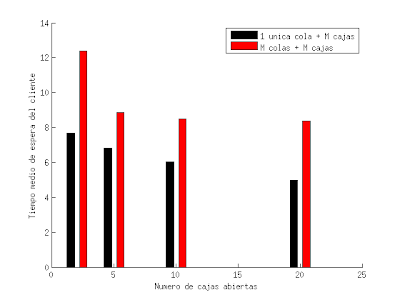(clic para ampliar)

Se ve claramente que ya desde sólo dos cajas se nota una disminución de hasta el 33% en el tiempo de espera. ¡Con los mismos recursos materiales y de personal, sólo cambiando la organización de la cola!

Aunque en el mundo real existan complicaciones que no se tienen en cuenta en este modelado matemático, como horas punta, creo que merecería la pena que todas las grandes superficies que físicamente puedan implementar este sistema se lo plantearan seriamente.


NOTA (25/MAR, 9:50am): El modelo de cola empleado cada vez que llega un cliente es el siguiente:

• Si hay una caja libre y sin cola delante, va a esa caja.
• En caso contrario, se va a la caja que no tenga cola. 
• Y en caso de no existir ninguna cola vacía, se elije una cola al azar con distribución uniforme.

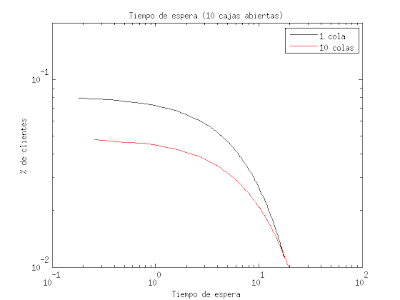
Para los de gustos matemáticos: Os dejo algunos histogramas (en escala logarítmica) para M=2, M=10 y M=20, donde se ve que la diferencia se va haciendo cada vez más grande al aumentar el número de cajas (M):

Nota: En las simulaciones se ha usado Período_llegada_clientes=1, Período atención en cada=M * Período_llegada_clientes * 0.9, para modelar el hecho de que si hay más cajas abiertas en un estado de equilibrio es porque se tarda más con cada cliente.
Fuente:

Ciencia Explicada